请大师们看看如下的一道几何题

踏歌而来

E,F是边长为3的正方形ABCD的边AD上两个点，且AE=DF，连接CF交BD于G，连接BE交AG于点H，若CH:CE=9：10，则AE=？

其妙

大师，

战巡

回复 1# 踏歌而来



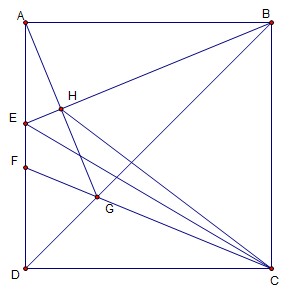
没啥难的吧...
首先易证$△DCG≌△ADG, △ABE≌△CDF, ∠DCF=∠DAG=∠ABE$，可证$AH⊥BE$
余弦定理可知：
\[\frac{BH^2+BC^2-2\cos∠CBH·BH·BC}{BE^2+BC^2-2\cos∠CBH·BE·BC}=\frac{CH^2}{CE^2}=\frac{81}{100}\]
令$∠CBH=∠BEA=∠BAH=\theta$
\[\frac{\frac{BH^2}{AB^2}+1-2\cos(\theta)\frac{BH}{AB}}{\frac{BE^2}{AB^2}+1-2\cos(\theta)\frac{BE}{AB}}=\frac{81}{100}\]
\[\frac{\sin^2(\theta)+1-2\cos(\theta)\sin(\theta)}{\frac{1}{\sin^2(\theta)}+1-\frac{2\cos(\theta)}{\sin(\theta)}}=\frac{81}{100}\]
化简得到
\[\sin^2(\theta)=\frac{81}{100}\]
可知$\frac{AB}{BE}=\frac{9}{10}, AE=\frac{\sqrt{19}}{3}$

isee

回复 3# 战巡


哇，$\dfrac{AB}{BE}=\dfrac{9}{10}$，这个很美，还。

踏歌而来

回复 3# 战巡

您很厉害！谢谢您！
请问如果不用余弦定理，是否可以求出。
因为这是一道初中数学的几何填空题。
从人教初中论坛上获得的。

战巡

回复 5# 踏歌而来


唉，就知道你们这帮人要求多...............
本人比较懒，余弦定理相对无脑，没那么多弯弯绕

不想用的话去证相似吧，射影定理可知$BH·BE=AB^2=BC^2$，后有$△BCH∽△BEC$
本人懒，后面略...........

isee

回复  踏歌而来



没啥难的吧...
首先易证$△DCG≌△ADG, △ABE≌△CDF, ∠DCF=∠DAG=∠ABE$，可证$AH⊥B ...
战巡 发表于 2014-3-10 09:29

战巡就是我偶像啊。

根据结果，有如下，纯几法。

$AH\perp EB$ 是必须证的，则\[AB^2=BH \cdot BE =BC^2 \Rightarrow \triangle BHC \sim \triangle BCE \]

这样便有 楼上那个$9:10$。


这样看，过度包装的图形，无趣……

isee

回复  踏歌而来


唉，就知道你们这帮人要求多...............
本人比较懒，余弦定理相对无脑，没那么多弯 ...
战巡 发表于 2014-3-10 10:42

哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈

三角法与题多配啊，美不胜收，继续继续发扬

PS：回复后看到你已经更新结果


PPS：这些共圆也很漂亮。

乌贼

我一直在找$CE:CH$的关系，原来是$\triangle BHC\sim\triangle BCE$

isee

回复 9# 乌贼


      图很多干扰线段，没办法啊，和战巡一样，强算，算完，再美化一下。像战巡愿意动手且把结果算出来的没几个的，至少，我只是脑子一闪，就过了

      所以，感谢那些无私写过程答题者

踏歌而来

我试了下暴力方法。
设CE=10m，CH=9m，AE=x
过E作EL垂直BC于L，过H作MN垂直BC交AD于M，BC于N。
在Rt△ABE中，BE＝√（9＋x^2），HE＝AE^2/BE=X^2/√(9+x^2)。
而sin∠AEB＝3/√(9+x^2)，cos∠AEB＝x/√(9+x^2)，
ME＝HEcos∠AEB＝x^3/(9+x^2)，
HM＝HEsin∠AEB＝3x^2/(9+x^2)，
所以有
由勾股定理HN^2+NC^2=CH^2,即
[3－3x^2/(9+x^2)]^2+[3-X+x^3/(9+x^2)]^2=(9m)^2  ①
由勾股定理EL^2+LC^2=EC^2，即
9＋(3－x)^2=(10m)^2  ②
联立①、②，从理论上可以求出x。

乌贼

回复 10# isee
这题我只有建系，硬算

isee

无所谓了，纯几也好，解析也好，至于喜欢那一个，我觉得，那  真 是个人偏好。

isee

我试了下暴力方法。
设CE=10m，CH=9m，AE=x
过E作EL垂直BC于L，过H作MN垂直BC交AD于M，BC于N。
在Rt△ABE中 ...
踏歌而来 发表于 2014-3-10 11:44

看看置顶的LaTeX代码吧，仅仅只在式子两端加美元符号就基本成了

如，适当各式单独对待，则





实际效果：

我试了下暴力方法。 by 踏歌而来
设$CE=10m，CH=9m，AE=x$

过$E$作$EL$垂直$BC$于$L$，过$H$作$MN$垂直$BC$交$AD$于$M$，$BC$于$N$。

在$Rt△ABE$中，$BE＝√（9＋x^2），HE＝AE^2/BE=X^2/√(9+x^2)$。

而$ sin∠AEB＝3/√(9+x^2)，cos∠AEB＝x/√(9+x^2)，$

$ME＝HEcos∠AEB＝x^3/(9+x^2)，$

$HM＝HEsin∠AEB＝3x^2/(9+x^2)，$

所以有

由勾股定理$HN^2+NC^2=CH^2$,即

$[3－3x^2/(9+x^2)]^2+[3-X+x^3/(9+x^2)]^2=(9m)^2$  ①

由勾股定理$EL^2+LC^2=EC^2$，即

$9＋(3－x)^2=(10m)^2$  ②

联立①、②，从理论上可以求出$x$。


再将根号，三角函数等部分常用数学符号换成对应代码就很好看了（如果愿意的话），不愿意也无所谓，

文字，主要是交流，不是美观，哈哈

踏歌而来

也许，实际上解不出来。
我再换成角度，看看是否可行。

延长$AG交CD于P，令∠DAP＝θ$，
由正方形的对称性可知，$AE＝DP＝ADtanθ＝3tanθ，BE＝AP＝AD/cosθ＝3/cosθ$，
$HE＝AE^2/BE=(3tanθ)^2/(3/cosθ)=3(tanθ)^2cosθ$，
$MH＝HEcosθ＝3(tanθ)^2(cosθ)^2，ME＝HEsinθ＝3(tanθ)^2cosθsinθ$，
$[3-3(tanθ)^2(cosθ)^2]^2+[3-3tanθ＋3(tanθ)^2cosθsinθ]^2=(9m)^2   ①$
$(3-3tanθ)^2+3^2=(10m)^2  ②$

$①/②并化简得(cosθ)^2＝81/100，$
$cosθ＝9/10。$
后面从略。