2D 引力定律

hbghlyj

根据Gauss's flux theorem, 二维的引力的模长与距离成反比, 三维的引力的模长与距离的平方成反比

vc.pdf page7

Example 4.1.
    $\cdots\ \cdots$
In a planar universe, the gravitational force field exerted by a point mass concentrated at the origin has, according to Newtonian gravitational theory, magnitude proportional to† $1/r$, where $r = \| x \|$ is the distance to the origin, and is directed towards the origin. Thus, the vector field describing gravitational force has the form$$\tag{4.1}\mathbf{f}=-\gamma \frac{\mathbf{x}}{\|\mathbf{x}\|}=\left(\frac{-\gamma x}{\sqrt{x^{2}+y^{2}}}, \frac{-\gamma y}{\sqrt{x^{2}+y^{2}}}\right)^{T}$$where $γ > 0$ denotes the constant of proportionality, namely the product of the two masses times the universal gravitational constant. The same force law applies to the attraction, $γ > 0$, and repulsion, $γ < 0$, of electrically charged particles.

---

† In three-dimensional Newtonian gravity, $1/r$ is replaced by $1/r^2$


page10
the gradient of the logarithmic potential function
\[
u(x, y)=-\gamma \log r=-\frac{1}{2} \gamma \log \left(x^2+y^2\right)
\]
is the gravitational force (4.1) exerted by a point mass concentrated at the origin.



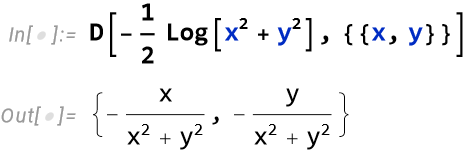
Newtonian gravity equation in a 2 dimensional world
Formally, you could write for circles around the point mass $C_1$ and $C_2$:
$$\int_{C_1}\vec F\left(r_1\right)\cdot \mbox{d}\vec s=\int_{C_2}\vec F\left(r_2\right)\cdot\mbox{d}\vec s$$
By rotational symmetry, this can be written as:
$$2\pi r_1 F_1=2\pi r_2 F_2 \Rightarrow F_2r_2=F_1r_1$$

See also. physics.stackexchange.com/questions/32779

hbghlyj

page 8

Newton's Laws of planetary motion produce the second order system of differential equations
\[
m \frac{d^2 \mathbf{x}}{d t^2}=\mathbf{f} .
\]
The solutions $\mathbf{x}(t)$ describe the trajectories of planets subject to a central gravitational force, e.g., the sun. They also govern the motion of electrically charged particles under a central electric charge, e.g., classical (i.e., not quantum) electrons revolving around a central nucleus. In three-dimensional Newtonian mechanics, planets move along conic sections–ellipses in the case of planets, and parabolas and hyperbolas in the case of non-recurrent objects like some comets. Interestingly (and not as well-known), the corresponding 2-dimensional theory is not as neatly described–the typical orbit of a planet around a planar sun does not form a simple closed curve! ^[3]
_______________
^[3] Dewdney, A.K., The Planiverse. Computer Contact with a Two-dimensional World, Copernicus, New York, 2001.
Libgen