来自人教群的三角最值——实为陈题改编

kuing

皖A教师xlnx(4012****) 2015-5-12 10:32:46

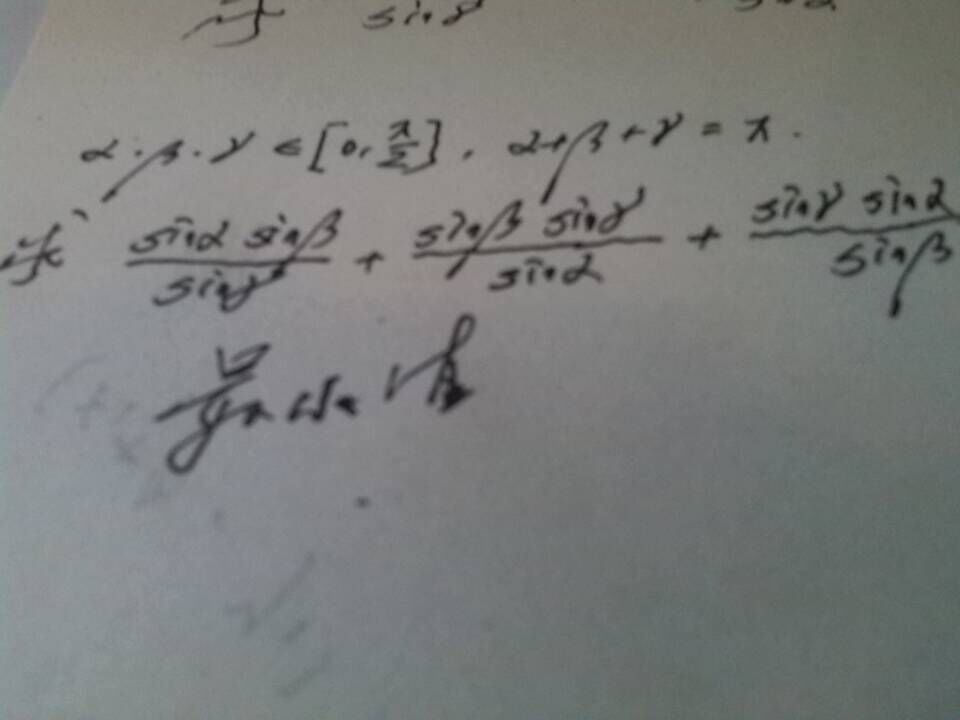
求教

首先显然变量不能为零，否则分母为零，估计楼主抄错了。

令 $\alpha=(\pi-A)/2$, $\beta=(\pi-B)/2$, $\gamma=(\pi-C)/2$，则由 $\alpha$, $\beta$, $\gamma \in (0,\pi/2]$, $\alpha +\beta +\gamma =\pi$ 得 $A$, $B$, $C\in [0,\pi)$, $A+B+C=\pi$，则
\[\frac{\sin \alpha \sin \beta }{\sin \gamma }=\frac{\cos \frac A2\cos \frac B2}{\sin \frac{A+B}2}=\frac1{\tan \frac A2+\tan \frac B2},\]
注意到恒等式
\[\tan \frac A2\tan \frac B2+\tan \frac B2\tan \frac C2+\tan \frac C2\tan \frac A2=1,\]
所以问题变成：$x$, $y$, $z\geqslant 0$, $xy+yz+zx=1$，求
\[\frac1{x+y}+\frac1{y+z}+\frac1{z+x}\]
的最小值，此乃陈题，证法不少，懒得再写（其中一种简证见附件： 一道数学竞赛题的直接证明_蒋明斌.pdf (37.23 KB, Downloads: 7076)

2015-5-12 13:27 Upload

Click on the file to download the attachment

）。
总之，结果是当 $x=0$, $y=z=1$ 时取最小值 $5/2$，
正好驳倒当时群里有人说：

这年头居然还有人迷信这种结论

kuing

沿着战巡说的

粤A爱好者战巡(3705*****) 2015-5-12 10:40:31
不等式请丢给色狼k
这玩意化简一下会变成2S(1/a^2+1/b^2+1/c^2)，这些玩意我不熟，某k应该知道会变成啥样

化边也可以化出来，由题设知，$\alpha$, $\beta$, $\gamma$ 可构成非钝角三角形，设该三角形的三边分别为 $a$, $b$, $c$，面积为 $S$，外接圆半径为 $R$，则由正弦定理及面积公式有
\[\sum\frac{\sin \alpha \sin \beta }{\sin \gamma }=\sum\frac{ab}{2Rc}=\frac{abc}{2R}\left( \frac1{a^2}+\frac1{b^2}+\frac1{c^2} \right)=2S\left( \frac1{a^2}+\frac1{b^2}+\frac1{c^2} \right),\]
令 $2x=b^2+c^2-a^2$, $2y=c^2+a^2-b^2$, $2z=a^2+b^2-c^2$，则由非钝角三角形知 $x$, $y$, $z\geqslant 0$，此时 $a=\sqrt{y+z}$, $b=\sqrt{z+x}$, $c=\sqrt{x+y}$，则
\begin{align*}
16S^2&=2a^2b^2+2b^2c^2+2c^2a^2-a^4-b^4-c^4 \\
& =2\sum(y+z)(z+x)-\sum(y+z)^2 \\
& =4(xy+yz+zx),
\end{align*}
所以
\[2S=\sqrt{xy+yz+zx},\]
代回去即得
\[\sum\frac{\sin \alpha \sin \beta }{\sin \gamma }=\sqrt{xy+yz+zx}\left( \frac1{x+y}+\frac1{y+z}+\frac1{z+x} \right),\]
于是同样也是等价于那道陈题。

kuing

突然想起旧版论坛也讨论过那道陈题，见 kkkkuingggg.haotui.com/thread-927-1-1.html （可惜现在旧版论坛要登录才能看到图片）
存档链接：kuingggg.github.io/5d6d/thread-927-1-4.html

kuing

回复 3# kuing

还是把链接中网友pxchg1200所说的简证写写吧。
两边平方等价于证
\[(xy+yz+zx)\left( \sum\frac1{(x+y)^2}+2\sum\frac1{(x+y)(y+z)} \right)\geqslant \frac{25}4,\]
由著名的Iran96不等式
\[(xy+yz+zx)\sum\frac1{(x+y)^2}\geqslant \frac94\]
可知只需证
\[(xy+yz+zx)\sum\frac1{(x+y)(y+z)}\geqslant 2,\]
即
\[(xy+yz+zx)(x+y+z)\geqslant (x+y)(y+z)(z+x),\]
显然成立。