转人教论坛的4个几何题

abababa

题一：在$\triangle ABC$中，$\angle B$和$\angle C$的内角平分线分别交$AC$和$AB$边于$M$和$N$，射线$MN$交$\triangle ABC$外接圆于$D$，试证:$\frac{1}{BD}=\frac{1}{AD}+\frac{1}{CD}$

题二：已知$\triangle ABC$为正三角形，$\odot O$是它的外接圆，$D$是劣弧$BC$上一点。$\odot P$和$\odot Q$分别是$\triangle ABD$和$\triangle ACD$的内切圆，它们的其中一条外公切线分别与$AB$、$AD$、$AC$交于$E$、$F$、$G$。
试证：
(1)$AF=FD$
(2)$EG=BE+CG$
(3)$PQ^2=BP^2+CQ^2$

题三：已知：$\triangle ABC$中，$\angle A=90^\circ$，$AD$切$\odot ABC$，$AD$交$BC$延长线于点$D$，$E$是$A$关于$BC$的对称点，$AY\perp BE$于$Y$，$X$是$AY$的中点，延长$BX$交$\odot ABC$于$J$，求证：$BD$切$\triangle AJD$的外接圆．

题四：已知四边形$ABCD$内接于以$DB$为直径的圆，设$A'$为$A$关于$BD$的对称点，$B'$是$B$关于$AC$对称点，直线$AC$交$DB'$于$Q$，直线$DB$交$CA'$于$P$，求证：$PQ\perp AC$

上面四题已经看过网友的证明了，想看看更“平几”的证法。

abababa

第三题人教论坛已经看到平几证法了，转过来。最开始看到的是三角函数方法证的。

bbs.pep.com.cn/forum.php?mod=viewthread&t … 274&extra=page=1

abababa

题四也在人教论坛看到了几何解法，转过来
bbs.pep.com.cn/forum.php?mod=viewthread&t … 274&extra=page=1

abababa

题四一位网友分别给出了坐标方法和几何方法，坐标方法看不懂，几何方法贴上来，但是字母与原题标得不一样。

abababa

题三转网友的解三角方程方法

isee

题1与题2还未解决

abababa

回复 6# isee

题一和题二也已经被网友解决了，题二他用了很多计算，题一他是用齐次坐标法做的，都不太“平几”化，主要是想看看平几方法。

乌贼

楼主，题一有平几解法吗？发上来学习。
另，题一：再延长$ NM $交外接圆于$ E $，$ O $为$ \triangle ABC $外接圆圆心，$ O_1 $为$ BC $边上旁切园圆心，
则有：$ OO_1 $垂直平分$ DE $

变式：题二：延长$BM$交园于$E$，连接$DE$交$AC$于$G$，再延长$BC$至$F$使$CF=AC$。求证：$G、E、B、F$四点共圆。

  题三 ： 如图，$ \triangle  ABC $中，$ E、F $分别是$ AB、AC $上的点且$ BE=EF=FC $，$ \angle AEF $的角平分线交$ AF $于$ N $ ，$\angle AFE $的角平分线交$ AE $于$ M $。求证：$ MN \px BC $


题三：由角平分线定理及$ NE\px BF，MF\px EC $有\[ \begin{align*}
&\dfrac{AM}{ME}=\dfrac{AF}{EF}\\
&\dfrac{AN}{NF}=\dfrac{AE}{EF}
\end{align*}\riff  \dfrac{AM}{AN}=\dfrac{AF}{NF}\cdot \dfrac{ME}{AE}\riff \dfrac{AM}{AN}=\dfrac{AB}{AE}\cdot \dfrac{CF}{AC}=\dfrac{AB}{AC}\]所以$MN\px BC$

abababa

回复 8# 乌贼

纯平几的暂时我没见到过，网友是用的坐标法解的，但中间的表达式也挺长的。主要的辅助线是$MN$与外接圆的交点，以及这点对三角形的西摩松线。

找到网友当时的证明了，latex 版的，发在下边：

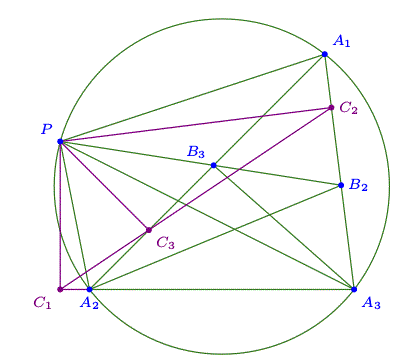
设$P$的 Simson 线为$C_1C_2C_3$。由于$\frac{PC_3}{PA_1} = \sin\angle PA_1A_2 = \sin\angle PA_3A_2 = \frac{PC_1}{PA_3}, \frac{PC_2}{PA_3} = \sin\angle PA_3A_1 = \sin\angle PA_2A_1 = \frac{PC_3}{PA_2}$，所以$\frac{1}{PA_3}+\frac{1}{PA_1}-\frac{1}{PA_2} = \frac{1}{PA_3}+\frac{PC_1}{PA_3 \cdot PC_3}-\frac{PC_2}{PA_3 \cdot PC_3} = PA_3 \cdot PC_3(PC_3+PC_1-PC_2)$。
易知$B_2 = (1,0,1), B_3 = (1,1,0)$，所以$B_2B_3 = (-1,1,1)$。设$P$点坐标为$(x,y,z)$，则$P$满足
$\begin{cases}
\begin{bmatrix}
x\\ y\\ z
\end{bmatrix} \cdot \begin{bmatrix}
-1 & 1 & 1
\end{bmatrix} = 0 & P\text{在}B_2B_3\text{上}\\
\begin{bmatrix}
x\\ y\\ z
\end{bmatrix} \cdot \begin{bmatrix}
0 & a_3 & a_2\\
a_3 & 0 & a_1\\
a_2 & a_1 & 0
\end{bmatrix} \cdot \begin{bmatrix}
x & y & z
\end{bmatrix} = 0 & P\text{在外接圆上}
\end{cases}$

解得$(x,y,z) = (-a_1-a_2+a_3\pm\sqrt{(a_1+a_2-a_3)^2+4a_1a_3}, -a_1-a_2-a_3\pm\sqrt{(a_1+a_2-a_3)^2+4a_1a_3}, 2a_3)$，于是对任意$k$都有$ky+kz-kx = 0$，由于$(PC_1, PC_2, -PC_3) = P = (kx,ky,kz)$，于是$PC_3+PC_1-PC_2 = 0$。

所以$\frac{1}{PA_3}+\frac{1}{PA_1}-\frac{1}{PA_2} = PA_3 \cdot PC_3(PC_3+PC_1-PC_2) = 0$。

乌贼

看不懂，另能给人教链接吗？

abababa

回复 10# 乌贼

时间太久了，我又不怎么会搜索，查不到了。应该是在人教论坛初中版的。不过初中版貌似现在好多垃圾帖
登录了一下，现在我居然连看图都看不了了。
本帖子中包含更多资源
您所在的用户组无法下载或查看附件

乌贼

回复 11# abababa
谢谢

kuing

时间太久了，我又不怎么会搜索，查不到了。应该是在人教论坛初中版的。不过初中版貌似现在好多垃圾帖
登录了一下，现在我居然连看图都看不了了。 ...
abababa 发表于 2017-5-24 14:31

人教渣坛那糟糕的管理和设置我已经无力吐槽

乌贼

西摩松线:
           baike.baidu.com/link?url=z0U5A12AjRtfSKGaIKst … -WssLr6pKBkYdM__ecCQ
鸡爪定理:
          baike.baidu.com/link?url=4QHu99mj-rMi8W7oRgNP … UJdPVDig5sXvhFkzdlZB
  
学习了

乌贼

回复 11# abababa
人教连接：
  bbs.pep.com.cn/forum.php?mod=viewthread&t … ine&orderby=dateline
没人回复，放在初中版，开玩笑了

乌贼

如图一：延长$ BC $至$ C_1 $使$ CC_1=AC $，作$ C_1A_1\px AC $交$ BA $于点$ A_1 $，作$ \triangle A_1BC_1 $外接圆$ O_1 $。延长$ BM $分别交园$ O、O_1、A_1C_1 $于$ E、M_1、E_1 $，连接$ AC_1、AM_1 $，延长$ M_1A $交园$ O_1 $于$ D_1 $，连接$DE $ 交 $AC $于$ F $，连接$D_1E_1 $ 交 $A_1C_1 $于$ F_1 $。易知：$B、D、D_1 $三点共线，  $B、F、F_1 $三点共线。
现证明$ D_1、F、C_1 $三点共线。

有事闪人，稍后继续……

如图二：连接$ D_1F $，
$ \angle D_1F_1A_1=\angle D_1BE_1 $有$ D_1、F_1、M_1、B $四点共圆，有$ \angle BF_1M_1=\angle BD_1A=\angle AFF_1 $（$AC \px A_1C_1 $），故\[ \angle BD_1F=\angle BCA =\angle BA_1C_1\]
再连接$ D_1C_1 $有\[ \angle BD_1C_1=\angle BA_1C_1=\angle BD_1F \]所以$ D_1、F、C_1 $三点共线且$ D_1C_1\px DC $
设$ D_1F $与$ AB $的交点为$ K $有$ \angle FKA=\angle CDA\riff\angle KDF=\angle KFD \riff DK=KF$
又\[ \angle AKC_1=\angle AD=\angle CABC \]有四点$ A、K、B、C_1 $共圆，有$ \angle DKB=\angle AC_1B=\angle NCB ( NC\px AC_1) \riff DB=DK=KF$
在$ AB $上取一点$ P $使$ \angle ADP=\angle CDB $有\[ \triangle ADP\sim \triangle CDB\riff\dfrac{AD}{DP}=\dfrac{CD}{DB} \]又\[ \angle AFK=\angle ACD=\angle ABD \\\angle PDB=\angle ADC=\angle AKF \\KF=DB\]有\[ \triangle AKF\cong \triangle PDB\riff DP=AK\riff PD=AD-DB \]所以\[ \dfrac{AD}{DA-DB}=\dfrac{DC}{DB}\riff \dfrac1{DB}=\dfrac1{DC}+\dfrac1{DA} \]
不知严谨否，感觉还可简练些……
人教那边不能连接这

乌贼

题二结论不美，不想作

abababa

回复 15# 乌贼

哦，一点你发的链接，然后什么都不点，再直接点“初中数学论坛”，就能看到那帖了，题二和题一是挨着的。

abababa

回复 16# 乌贼

其实这题要是按9楼网友做的，按9楼里给的图，点P在外接圆上只是把$PA_1,PA_2,PA_3$转成$PC_1,PC_2,PC_3$，后面都不需要方程组里第二个方程，因为从那个方程组的第一个方程，就能确定总是有$PC_3+PC_1-PC_2=0$，这只需要点$P$在$B_2B_3$上就行。

乌贼

回复 8# 乌贼
如图：
设$ BM、CN $交点为$ J $，作$ \triangle BJC $外接圆$ O_1 $，延长$ AJ $交园$ O_1 $于$ H $，分别作$ \triangle ACH 、\triangle ABH$外接圆$ O_2、O_3 $，分别延长$ CD、AB $交园$ O_2 $于$ P、Q $，再延长$ AC $交园$ O_3 $于$ G $，易证：\[ \begin{align*}
&AD=DP\\&BQ=BC=CG
\end{align*} \]
再延长$ DB $交园$ O_3 $于$ K $，连接$ AK、BG $有\[ \begin{align*}
\angle AKD=\angle AGB\\\angle ADK=\angle BCG
\end{align*}\riff \triangle ADK\sim \triangle BCG\riff DK=AD=DP \]
连接$ PQ,QG $有\[ \angle QPC=\angle QAC=\angle BDC\riff PQ\px BD \]
易证：(见回复8楼题三)\[ MH\px QG \]
又延长$ CB,AD $分别交$ PQ $于$ E,F $两点(可能重合)，则\[ \angle AEF=\angle ACF \]
因\[ \dfrac{AM}{MC}=\dfrac{AB}{BQ}=\dfrac{AD}{DF} \riff DM\px FC\px QG\riff  \angle AEF=\angle ACF =\angle AGQ \]
所以$ A,E,Q,H $四点共圆。连接$ EG $，有\[ \angle QEG=\angle QAG =\angle BDC=\angle QPC \riff PC\px EG\]
连接$ KG $由\[ \angle BKG+\angle BAC=\angle BKG+\angle BDC=180\du \riff\\\begin{align*}
&DC\px KG\\&PC\px EG
\end{align*}  \]
故$ E,K,G $三点共线，有$ PEKD $为平行四边形，得\[ PE=KD=AD=PD \]
因此\[ \dfrac{CD}{BD} =\dfrac{PC}{PE}\riff \dfrac1{BD} =\dfrac{PD+CD}{AD\cdot CD}=\dfrac1{CD}+\dfrac1{AD} \]