|
|
original poster
hbghlyj
posted 2023-1-25 22:31
Last edited by hbghlyj 2023-2-5 16:49公式的推导在
P. Poulet, Reply to Query 4750, Permutations, L'Intermédiaire des Mathématiciens, v.26 (1919), 117-121.
第26卷的Google Book链接因版权限制,只能搜索文本,不能查看全文.
有人在MathOverflow上问过哪里可以下载 L'Intermédiaire des Mathématiciens 这个journal.
Hathitrust有第26卷但因版权限制无法下载
第17卷在Archive可以看,但是没有找到所需的第26卷
在Numdam也没有搜到.







| 4750 (1947,78)(G. Metrod). — Permutations. —Cherchons d'abord à préciser l'énoncé de la question qui présente quelque ambiguïté. Si nous disons, en effet:
Parmi toutes les permutations des $n$ premiers nombres entiers, combien y en a-t-il telles que la différence en valeur absolue de deux termes consécutifs soit différente de l'unité?
Nous voyons que pour $n=4$ les permutations 2413 et 3142 répondent à la question, alors que l'auteur affirme qu'il n'en eviste pas. La question doit sans doute être ainsi comprise:
Parmi toutes les permutations des $n$ premiers nombres entiers, combien y en a-t-il telles que la différence en valeur absolue de deux termes consécutifs ou des termes extrêmes soit différente de 1 et de $n-1$ ?
L'avantage de ces restrictions supplémentaires est d'établir une symétrie parfaite entre tous les termes de la permutation. Le problème devient alors le mème que le suivant:
Étant donnés $n$ points sur un contour fermé, quel est le nombre des polygones que l'on peut former avec ces $n$ points pour sommets, sans qu'aucun cólé joigne deux sommets consécutif sur le contour?
A chacun des polygones correspondent, en effet, $2n$ des permutations considérées.
Nous allons d'abord résoudre le problème aınsi posé; nous en déduirons, aisément du reste, la solution du premier énoncé.
Si nous appelons, pour abréger, côte simple du polygone un côté joignant deux sommets consécutifs, nous pouvons, d'une façon plus générale, chercher à calculer le nombre $\gamma_n^k$ des polygones de $n$ côtés, ayant $k$ côtés simples, et le nombre $\Gamma_n^k$ des permutations correspondantes, égal à $2n\gamma_n^k$.
Voici le Tableau de ces valeurs pour $n \leqq 11$ : |
n $γ_n^0$ $γ_n^1$ $γ_n^2$ $γ_n^3$ $γ_n^4$ $γ_n^5$ $γ_n^6$ $γ_n^7$
0 1
1 0 1
2 0 0 1
3 0 0 0 1
4 0 0 2 0 1
5 1 0 5 5 0 1
6 3 12 15 20 9 0 1
7 23 70 112 91 49 14 0 1

| Pour construire ce Tableau, il suffit de connaitre des formules de récurrence reliant chacun des termes de la $n^{\text {ème}}$ ligne à ceux des lignes antérieures.
Nous avons obtenu de telles formules par trois méthodes qui se complètent l'une l'autre, et que nous donnons ci-dessous avec les résultats qu'elles nous ont fournis, mais sans entrer dans le détail des démonstrations qui sont un peu longues et qui demandent plus d'attention que de sagacité. |
$1^{\circ}$ On considére une permutation particulière de $n-1$ termes, et l'on cherche, par l'intercalation du terme $n$, à obtenir une permutation de $n$ termes correspondant à un polygone ayant $0, 1,2, \ldots,n$ côtés simples.
En opérant ainsi, nous a vons trouvé les formules
$$\leqalignno{\gamma_n^0=&(n-1) \gamma_{n-1}^0+2 \frac{(n-4)}{(n-1)} \gamma_{n-1}^1+\frac{2}{n-1} \gamma_{n-1}^2-\frac{2}{n-2} \gamma_{n-2}^1&(1)\\
\gamma_n^1 = &4 \gamma_{n-1}^0+\frac{n^2-8 n+18}{n-1} \gamma_{n-1}^1+\frac{4(n-5)}{n-1} \gamma_{n-1}^2 &(2)\cr
&+\frac{6}{n-1} \gamma_{n-1}^3+\frac{6}{n-2} \gamma_{n-2}^1-\frac{4}{n-2} \gamma_{n-2}^2&
}
$$
Ces formules ne doivent pas ètre employées pour $n<5$, car elles résultent de la simplification d'expressions plus étendues, dans lesquelles certains termes se présentent alors avec des coefficients négatifs, alors qu'ils doivent ètre simplement égalés à zéro. Cette remarque est générale.
$2^{\circ}$ On considère toutes les permutations qui commencent par 12 et qui correspondent à des polygones ayant $k$ côtés simples, dont le nombre est évidemment $\frac{k}{n} \gamma_n^{k}$; si l'on supprime le chiffe 1, les permutations restantes ont $n-1$ termes consécutifs et correspondent, suivant les cas, à des polygones ayant $k-1, k$ ou $k+1$ côtés simples, qu'il suffit de compter. Nous avons ainsi obtenu la formule générale suivante:\[\leqalignno{ \frac{k \gamma_{n}^{k}}{n}= & \frac{2(n-k)}{n-1} \gamma_{n-1}^{k-1}+\frac{2 k}{n-1} \gamma_{n-1}^{k}+\frac{k-2}{n-2} \gamma_{n-2}^{k-2} &(3)\\ & -\frac{2(k-1)}{n-2} \gamma_{n-2}^{k-1}+\frac{k}{n-2} \gamma_{n-2}^{k}}\]
Pour $k=1$ et $k=2$, cette formule se réduit à
\[\leqalignno{\frac1{n} \gamma_n^{1}&=2 \gamma_{n-1}^{0}+\frac{2}{n-1} \gamma_{n-1}^{1}+\frac1{n-2} \gamma_{n-2}^{1} &(4)\\ \frac{1}{n} \gamma^2_n&=\frac{n-2}{n-1} \gamma_{n-1}^{1}+\frac{2}{n-1} \gamma_{n-1}^{2}-\frac{1}{n-2}\left(\gamma_{n-2}^{1}-\gamma_{n-2}^{2}\right)&(5)}\]

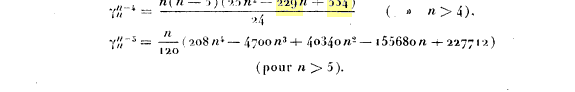
| $3^\circ$ Pour les valeurs de $k$ voisines de $n$, l'examen direct des polygones donne\begin{align*}\gamma_n^n&=1\\\gamma_n^{n-1}&=0\\\gamma_{n}^{n-2}&=\frac{n(n-3)}{2}&(\text{pour }n>2)\\\gamma_{n}^{n-3}&=\frac{2 n(n-4)(2 n-1)}{6}&(\text{pour }n>3)\\\gamma_n^{n-4}&=\frac{n(n-1)\left(25 n^2-229 n+534\right)}{24} &(\text{pour }n>4)\\\gamma^{n-5}_n&=\frac{n}{120}\left(208 n^4-4700 n^3+40340 n^2-155680 n+227712\right)&(\text{pour }n>5)\end{align*}
|


| De ces diverses formules, on peut évidemment déduire quantité d'autres; mais les formules (1), (4) et (5) suffisent pour la résolution des problèmes posés, puisqu'elles permettent-de calculer les trois premières colonnes du Tableau, indépendamment des autres. On peut mème en tirer des formules qui ne renferment que des termes d'une même colonne. Nous trouvons ainsi$$\leqalignno{\gamma_{n+2}^{0}&\left(n^{2}-3 n-1\right)-\gamma^{0} n+1\left(n^{3}-2 n^{2}-2 n-9\right)&(6) \\& -4\gamma_n^{0}(n-3)(n+2)+2 \gamma^{0}_{n-1}(n-4)\left(n^{2}-n-3\right) \\ &-\gamma_{n-2}^{0}\left(n^{2}-3 n-1\right)-\gamma_{n-3}^{0}(n-3)\left(n^{2}-n-3\right)=0 \quad(n>5)\\\frac{\gamma_{n+2}^{1}}{n-2}&-\frac{n}{n+1} \gamma_{n+1}^{1}-\frac{4}{n} \gamma_n^{1}+\frac{2(n-3)}{n-1} \gamma_{n-1}^{1} -\frac{1}{n-2} \gamma_{n-2}^{1}-\frac{n-2}{n-3} \gamma_{n-3}^{1}=0&(7)}$$ |
Ces formules ne sont peut-ètre pas les plus simples qu'on puisse trouver.
Si nous revenons maintenant à notre premier énoncé, nous voyons qu'il faut ajouter aux permutations $\Gamma_n^0$ les permutations $\Gamma_n^1$, qui ont, soit entre leurs termes extrêmes une différence de 1 ou $n-1$, soit dans le corps de la permutation 1 et $n$ consécutifs, puis les permutations $\Gamma_n^2$ qui réunissent ces deux conditions. Leur nombre total $P_n$ est ainsi trouvé égal à
$$\leqalignno{&\Gamma_n^0+\frac{2 n-1}{n^2} \Gamma_n^1+\frac{2}{n^2} \Gamma_n^2&(8)}
$$
On a ainsi pour
\begin{array}l
n=4, \quad 5, \quad 6, \quad 7, \quad 8, \quad 9, \quad 10, \quad 11, \quad 12 \ldots \\
P=2,14,90, 646,5242,47622,479306,5296790,63779034 \ldots
\end{array}La combinaison de la formule (8) avec les formules précédentes nous donne encore
$$\leqalignno{P_n&=\frac{1}{n+2} \gamma_{n+2}^1+\frac{2}{n+1} \gamma_{n+1}^1+\frac{1}{n} \gamma_n^1&(9)\\
P_{n+1}&=(n+2)P_n-(n-1) P_{n-1}-(n-4) P_{n-2}+(n-2) P_{n-3} \quad(n>4)&(10)}$$P. Poulet |
|