Sequences of Polygons
Author(s): R. J. Clarke
Source: Mathematics Magazine , Mar., 1979, Vol. 52, No. 2 (Mar., 1979), pp. 102-105
Let $P$ be a convex polygon and let $T P$ be the polygon whose vertices are the midpoints of the sides of $P .$ We are interested in the sequence $P, T P, T^{2} P, \ldots$ If $P$ is a triangle, $T P$ is similar to $P$. If $P$ is a quadrilateral, $T P$ is a parallelogram; thereafter $T^{m} P$ is similar to $T P$ if $m$ is odd, to $T^{2} P$ if $m$ is even. For a pentagon, the situation is less simple. However, experimentation soon convinces us that $T^{m} P$ approaches a limiting shape, and that alternate members of this sequence "point" in opposite directions. We shall prove these facts for a general convex polygon $P$.
It is convenient to consider each vertex $v_{i}$ of $P$ as a complex number and to take$$P=\left[\begin{array}{c}v_{1} \\v_{2} \\\vdots \\v_{n}\end{array}\right]$$as a vector in $\Bbb{C}^{n} .$ We may then think of the operator $T$ as a matrix; in fact$$T=\frac{1}{2}\left[\begin{array}{cccccc}1 & 1 & 0 & \cdots & 0 \\ 0 & 1 & 1 & \cdots& 0 \\ 0 & 0 & 1 &\cdots&0\\\vdots&\vdots&\vdots&\ddots&\vdots\\1 & 0 & 0&\cdots & 1\end{array}\right]$$Define matrices $C$ and $A$ by$$C=\left[\begin{array}c0&1&0&\cdots&0\\0&0&1& \cdots&0\\\vdots&\vdots&\vdots&\ddots&\vdots\\0&0&0&\cdots&1\\1&0&0&\cdots&0\end{array}\right]$$and $A=C^{-1} T^{2}$, so that$$A=\frac{1}{4}\left[\begin{array}c2&1&0&\cdots&0&1\\1&2&1& \cdots&0&0\\0&1&2&\cdots&0&0\\\vdots&\vdots&\vdots&\ddots&\vdots&\vdots\\1&0&0&\cdots&1&2\end{array}\right]$$On considering the cases $n=4$ and $n=5$ we see that the sequence $\left\{A^{m} P\right\}$ is a judicious one to look at: the $T^{2}$ in $A$ enables us to look at every other polygon in the sequence $\left\{T^{m} P\right\}$, and the $C^{-1}$ labels the vertices of $T^{2} P$ conveniently (see Figure 1). Let $\zeta=\exp (2\pi i / n)$. Then $A$ has eigenvalues$$\lambda_{r}=\frac{1}{4}\left(2+\zeta^r+\zeta^{-r}\right), \text { for } r=0,1,2, \ldots n-1$$and eigenvectors$$P_r=\left[\begin{array}{l}1 \\ \zeta^r\\ \zeta^{2r} \\ \vdots \\ \zeta^{(n-1)r}\end{array}\right]$$since the $i$ th entry of $AP_r$ is\begin{aligned}\frac14\left(\zeta^{(i-2) r}+2 \zeta^{(i-1)r}+\zeta^{ir}\right)&=\lambda_r\zeta^{(i-1)r}\\&=\lambda_r\times i\text{ th entry of }P_r\end{aligned}Since the eigenvectors of $A$ are linearly independent, they form a basis for $\Bbb C^n$, so we may write $P=\sum_{r=0}^{n-1} \alpha_rP_r$ where $\alpha_r\in\Bbb C$. Then $A^mP=\sum_{r=0}^{n-1} \lambda_r^m\alpha_rP_r.$ If $0<r<n$, then $\left|\lambda_r\right|<\lambda_0=1 .$ So $A^{m} P \rightarrow\alpha_0P_0.$ An easy calculation shows that $\alpha_0P_0$ is the centroid of $P .$ Thus the sequence $\left\{A^mP\right\}$ and hence the sequence $\left\{T^mP\right\}$ tends to the centroid of $P$. It seems difficult to prove this point geometrically.
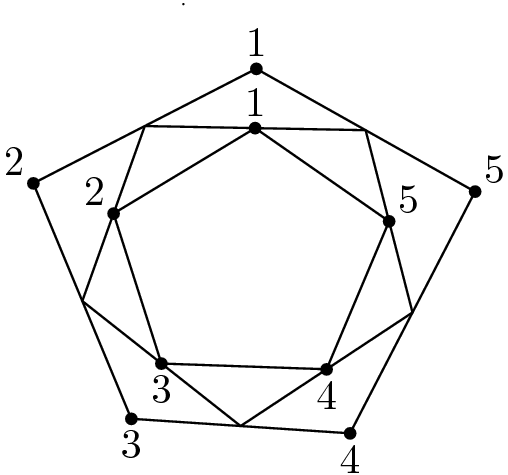
Figure. 1.Metapost代码
draw(0,80);
pair p[],q[],r[];
p1=50(0.35,1.29);
p2=50(-0.72,0.74);
p3=50(-0.25,-0.39);
p4=50(0.8,-0.46);
p5=50(1.4,0.7);
draw for j=1 upto 5:p[j]-- endfor cycle;
for j=1 upto 5:q[j]=1/2[p[j],p[j mod 5+1]];endfor
draw for j=1 upto 5:q[j]-- endfor cycle;
for j=1 upto 5:r[j mod 5+1]=1/2[q[j],q[j mod5+1]];endfor
draw for j=1 upto 5:r[j]-- endfor cycle;
dotlabel.top("1",p1);dotlabel.top("1",r1);
dotlabel.ulft("2",p2);dotlabel.ulft("2",r2);
dotlabel.bot("3",p3);dotlabel.bot("3",r3);
dotlabel.bot("4",p4);dotlabel.bot("4",r4);
dotlabel.urt("5",p5);dotlabel.urt("5",r5);
We now show that for any convex polygon $P$ we have $\alpha_{1}$ or $\alpha_{n-1}$ non-zero. Let $r$ be the smallest integer such that either $\alpha_{r}$ or $\alpha_{n-r}$ is non-zero. Then $A^{m} P / \lambda_{r}^{m} \rightarrow \alpha_{r} P_{r}+\alpha_{n-r} P_{n-r} .$ Hence the polygon on the righthand side is convex. Let $e_{k}$ be the $k$ th edge of $\alpha_{r} P_{r}+\alpha_{n-r} P_{n-r}$. Then $e_{k}=\alpha_{r} \Delta_{k}+\alpha_{n-r} \Delta_{k}^{\prime}$, where $\Delta_k=\zeta^{r(k+1)}-\zeta^{rk}$ is the $k$ th edge of $P_r$ and $\Delta_k'=\zeta^{-r(k+1)}-\zeta^{-r k}$ is the $k$ th edge of $P_{n-r}$. Then $\Delta_{k+1}=\left(\zeta^{r}+\zeta^{-r}\right) \Delta_k-\Delta_{k-1}$ for $1 \leqslant k \leqslant n-1$. Define a sequence of polynomials $F_{m}(x)$ by $F_{0}(x)=0, F_{1}(x)=1, F_{2}(x)=x$, and $F_{m+1}(x)=x F_{m}(x)-F_{m-1}(x)$ for $m \geqslant 1$. Then by induction we may show that
$$
\Delta_{k}=F_{k}\left(\zeta^{r}+\zeta^{-r}\right) \Delta_{1}-F_{k-1}\left(\zeta^{r}+\zeta^{-r}\right) \Delta_{0}, \quad 1 \leqslant k \leqslant n
$$and the same relationship holds among the $\Delta_{k}^{\prime}$ and among the $e_{k}$.
Consider the linear mapping of the plane that takes $e_{0}$ to $\Delta_{0}$ and $e_{1}$ to $\Delta_{1} .$ By the linear relationships above, the mapping takes $e_{k}$ to $\Delta_{k}$, i.e., it takes the polygon $\alpha_{r} P_{r}+\alpha_{n-r} P_{n-r}$ to $P_{r}$. Now the property of being convex is preserved under a linear transformation of the plane. But $P_{r}$ is not convex unless $r=1$, so the result follows: either $\alpha_{1}$ or $\alpha_{n-1}$ is non-zero.
We may call a polygon $P$ a limit polygon if $A P$ is similar to $P$. We now know that the limit polygons are those of form$$P=\alpha_{1} P_{1}+\alpha_{n-1} P_{n-1}\tag1$$These polygons can be characterized geometrically: they are just those polygons $P$, with vertices $v_{1}, \ldots, v_{n}$, for which there is a constant $c$ with$$v_{i+2}-v_{i+1}=c\left(v_{i+1}-v_{i}\right), \quad 1 \leqslant i \leqslant n\tag2$$We can easily verify that a polygon of form (1) has property (2) with $c=4 \lambda_{1}-1=1+$ $2 \cos (2 \pi / n)$, as $\lambda_{1}=\frac{1}{4}(\exp (2 \pi i / n)+\exp (-2 \pi i / n)+2)$. On the other hand one easily sees that a polygon with property (2) is a limit polygon.

Figure. 2.Metapost代码
draw(-10,110);
draw unitsquare scaled 100;
pair f[],g[];
p:=(sqrt(5)-1)/2;
f1=p[(0,0),(0,100)];
f2=(0,0);
f3=p[(0,0),(100,0)];
f4=p[(100,0),(100,100)];
f5=p[(0,100),(100,100)];
dotlabel.lft("1",f1);
dotlabel.llft("2",f2);
dotlabel.bot("3",f3);
dotlabel.rt("4",f4);
dotlabel.top("5",f5);
for j=1 upto 5: g[j]=1/2[f[j],f[j mod 5+1]];endfor
draw for j=1 upto 5: f[j]-- endfor cycle;
draw for j=1 upto 5: g[j]-- endfor cycle;
draw f1--f4..f3--f5 dashed evenly;
dotlabel.lft("4",g1);
dotlabel.bot("5",g2);
dotlabel.lrt("1",g3);
dotlabel.urt("2",g4);
dotlabel.ulft("3",g5);
We now show that if $n$ is odd, then the sequence of similarity classes $\left[T^{m} P\right]$ has the same limit as the sequence $\left[A^{m} P\right] .$ Define an operation $S$ by $S P=C^{(n-1) / 2} T P .$ Here we are just labelling the vertices of $T P$ so that the first vertex lies between the $\frac{1}{2}(n+1)$ th and $\frac{1}{2}(n+3)$ rd vertices of $P$. Clearly $S^2=A$. Now we have$$S P_{r}=\frac{1}{2}\left(\zeta^{\frac{1}{2}(n-1) r}+\zeta \frac{1}{2}(n+1) r\right) P_{r}, \quad \text { for } r=1,2,3, \ldots, n-1$$So if $P=\sum_{r=1}^{n-1} \alpha_{r} P_{r}$,
$$
S P=\frac{1}{2} \sum_{r=1}^{n-1} \alpha_{r}\left(\zeta^{\frac{1}{2}(n-1) r}+\zeta^{\frac{1}{2}(n+1) r}\right) P_{r} .
$$
So, with $\lambda_{1}=\frac{1}{2}\left(2+\zeta+\zeta^{-1}\right)$,\begin{aligned}
\left(\frac{1}{\lambda_{1}} A\right)^{m} S P & \rightarrow \frac{1}{2}\left(\zeta^{\frac{1}{2}(n-1)}+\zeta^{\frac{1}{2}(n+1)}\right)\left(\alpha_{1} P_{1}+\alpha_{n-1} P_{n-1}\right) \\
=&-\left(\cos \frac{\pi}{n}\right)\left(\alpha_{1} P_{1}+\alpha_{n-1} P_{n-1}\right) .
\end{aligned}Hence the sequence $\left[S^{m} P\right]$ has the same limit as $\left[A^{m} P\right]$.
The problem of midpoint polygons allows a natural generalization as follows. Let $f=a_{0}+$ $a_{1} x+\cdots+a_{d} x^{d}$ be a polynomial with non-negative real coefficients whose sum is 1 . Let $n$ be an integer greater than $d$ and let $T=a_{0} I+a_{1} C+\cdots+a_{d} C^{d}$, where $C$ is the matrix defined above. Then we ask if there are integers $k$ and $l$ such that for all $n$, and for all convex $n$-gons $P$, the sequence $\left[A(k, l)^{m} P\right]$ converges to a similarity class of convex polygons, where $A(k, l)=C^{-k} T^{l}$. If the answer is yes, we call $f(x)$ convergent. We have found above, in the midpoint problem, that the polynomial $\frac{1}{2}+\frac{1}{2} x$ is convergent.
Define a function $g(x)$ by $g(x)=x^{-k} f(x)^l$. Then $A$ has eigenvalues $g\left(\zeta^{r}\right)$, for $r=0, \ldots, n-1$, where $\zeta=\exp (2 \pi i / n)$, and eigenvectors $P_{r}$ as above. If we write $P=\sum_{r=0}^{n-1} \alpha_r P_r$ as usual we have $A P=\sum_{r=0}^{n-1} \alpha_r g\left(\zeta^{r}\right) P_r.$
By our assumption on the polynomial $f(x)$ we have $g(1)=1$ and $|g(\zeta^r)|<1$ if $r=1,2,3, \ldots$, $n-1$. So $A^{m} P \rightarrow \alpha_{0} P_{0}$ as before. Assume $\alpha_{0}=0$. Then necessary and sufficient conditions for the sequence $\left[A^{m} P\right]$ to have the required limit are that$$g(\zeta)=g\left(\zeta^{-1}\right)\tag3$$and$$\left|g\left(\zeta^{r}\right)\right|<|g(\zeta)| \text { if } r=2,3, \ldots, n-2\tag4$$We can rewrite these as$$ \zeta^{-k} f^{l}(\zeta)=\zeta^{k} f^{l}\left(\zeta^{-1}\right)\tag{3'}$$and$$\left|f\left(\zeta^{r}\right)\right|<|f(\zeta)| \text { if } r=2,3, \ldots, n-2\tag{4'}$$Now (3') implies that $x^{-k} f^{l}(x)-x^{k} f^{l}\left(x^{-1}\right)$ is divisible by $x-\zeta$ for every primitive $n$th root of unity $\zeta$, for all $n>d$. Hence $x^{-k} f'(x)=x^{k} f^{l}\left(x^{-1}\right)$. As $f'(x)$ has degree $d l$, we have that $d l$ is even and $k=d l / 2$. So $x^{-d / 2} f(x)=x^{d / 2} f\left(x^{-1}\right)$. Thus $a_r=a_{d-r}$ for $r=0,1,2, \ldots, d$. Such a polynomial is called a reciprocal polynomial. If the degree $d$ is even, we may satisfy (4), by taking $l=1$ and $k=d / 2$, while if $d$ is odd, we must take $l=2$ and $k=d$.
THEOREM. A polynomial $f(x)$ of degree $d$ is a convergent polynomial if and only if $f(x)$ is reciprocal and $\left|f\left(\zeta^{r}\right)\right|<|f(\zeta)|$ for $r=2,3, \ldots, n-2$, where $n>d$ and $\zeta=\exp (2 \pi i / n)$.
It follows, for instance, that the sequence of polygons obtained by trisecting the sides of a given polygon does not usually converge in the above sense.
We conclude by mentioning a related but apparently more difficult problem. Let $P$ be a convex pentagon and let $P^{\prime}$ be the pentagon formed by the intersections of the diagonals of $P$. What can we say about the sequence $P, P^{\prime}, P^{\prime \prime}, \ldots ?$ This problem is non-linear and therefore harder than the previous problems, although it may well have a similar solution. We have been able to make little progress on it. |