|
|
Last edited by hbghlyj 2023-2-5 13:48直径不超过1的凸图形$X$可由边长为$1/\sqrt3$的正六边形覆盖.
证:
称对边距离不超过1的等角六边形$ABCDEF$为好六边形(临时记号).
对于直径不超过1的凸图形$X$和角$θ∈[0, 60°]$,分别作倾角为$0, θ+60°, θ+120°$的三对平行的支撑线,设围成的凸六边形为$ABCDEF$ (逆时针),则其为好六边形.
若六条边均不超过,则由命题2知结论成立.若有边大于$1/\sqrt3$,不妨设$AB>1/\sqrt3$,则由命题1知$BC<1/\sqrt3$.当θ从0连续地变到60°时,$AB$也在连续变化,最终变为$BC$.因此存在$θ$使得$AB=1/\sqrt3$,由命题3知结论成立.
命题1.$AB+BC≤2/\sqrt3$
证:$AB\sin120°+BC\sin120° =d(FA,CD)≤1$
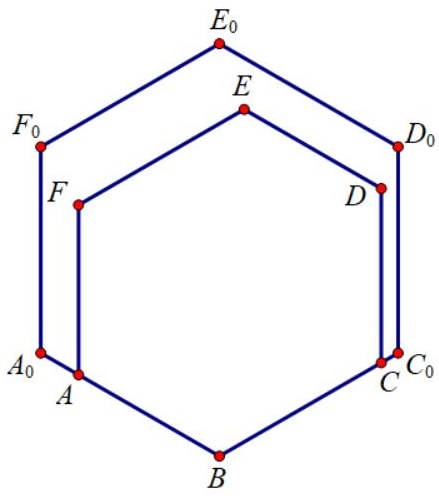
命题2.若$AB$和$BC$均不超过$1/\sqrt3$,则$ABCDEF$可被边长为$1/\sqrt3$的正六边形覆盖.
证:如图作边长为$1/\sqrt3$的正六边形$A_0 BC_0 D_0 E_0 F_0$,使$A$在$A_0 B$上,$C$在$C_0 B$上.则由好六边形的定义,可知$D,E,F$也在$A_0 BC_0 D_0 E_0 F_0$内部或边界上.
命题3.若$AB=1/\sqrt3$,则$ABCDEF$可被以$AB$为边的正六边形覆盖.
证:由命题1知$BC≤1/\sqrt3$,再由命题2即得证. |
|