factor a linear map $R^m→M$ to linear maps $R^m→R^n$ and $R^n→M$

hbghlyj

• $M$ is a $R$-module. Suppose that $φ:R^m→M$ and $ψ : R^n→M$ are $R$-linear maps. Show that if $φ$ is surjective then there is $A∈M_{n,m}(R)$ such that $φ(xA) = ψ(x)$ for all $x ∈ R^n$.
• Show that if $ψ$ is also surjective then the map\[Ψ : \ker φ → R^m/R^nA;   y↦y+R^nA\]is surjective and $\ker Ψ = \set{vA: v ∈\ker ψ}$. Why is $R^m/R^nA$ finitely generated?
• Deduce that if $\ker ψ$ is finitely generated then $\ker φ$ is finitely generated too.

Czhang271828

These are easy questions if you are allowed to take elements in a given module. In an arbitrary Abelian category (which means linear algebra), one can on longer take elements in any object. However, the statements in your questions still hold.

T1

(1) Hint: since ${_R}\mathrm{Mod}$ is an Abelian category, $(R^m,\varphi)$ is the kernel of $M\overset 0\longrightarrow 0$. Hence, for any $R^n\overset {\psi}\longrightarrow M$ such that $0\circ \psi =0$, there exists a unique $\theta:R^n\to R^m$ such that $\psi=\varphi\circ \theta$.

The kernel $(R^m,\varphi)$ is usually simplified into $R^m$ or $\varphi$.

Le diagramme est commutatif for the first part.  

Le diagramme commutatif de Ex.1

T2

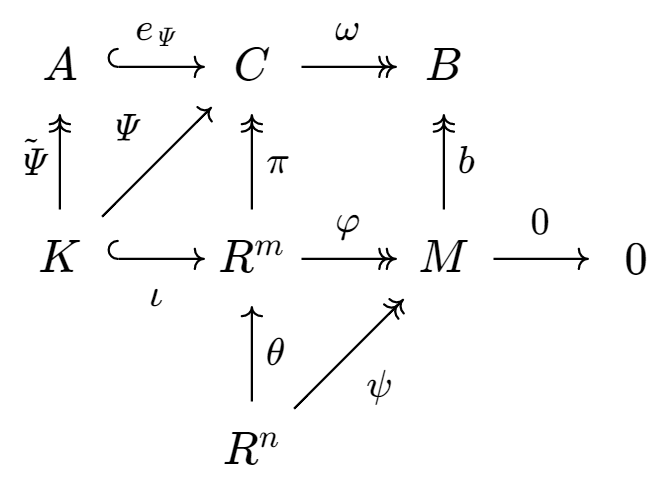
(2) Hint: Let $(C,\pi)$ be cokernel of $\theta$, $(K,\iota)$ be kernel of $\varphi$. Here $\varPsi$ is defined as the composition $\pi\circ \iota$. $K\overset{\tilde \varPsi}\twoheadrightarrow A\overset{e_\varPsi}\hookrightarrow C$ is the inject-surject decomposition of $\varPsi$. Therefore $(K\overset{\tilde \varPsi}\twoheadrightarrow A,(\iota,e_\varPsi))$ is the kernel of $R^m\overset\pi\twoheadrightarrow C$ in the corresponding morphism category ${_R}\mathrm{Mod}^\to$, $M\overset b\twoheadrightarrow B$ is the cokernel. The commutative diagram reveals that
$$
\omega\circ \pi\circ \theta=b\circ \psi:R^n\to B
$$
is surjective, but also zero ($\pi\circ \theta=0$ by definition of exact sequences). Thus $B=0$. The exactness of $A\overset {e_\varPsi}\hookrightarrow C\overset\omega\twoheadrightarrow B$ is induced by the exact sequence $\boxed{\substack{K\\\downarrow\\A}}\hookrightarrow \boxed{\substack{R^m\\\downarrow\\C}}\twoheadrightarrow \boxed{\substack{M\\\downarrow\\B}}$, hence $e_\varPsi$ is isomorphism. Consequently, $\varPsi$ is surjective.  

Morphism category = viewing morphisms as new objects.

Le diagramme est commutatif for the second part.

Le diagramme commutatif de Ex.2

The questions left are easy: in order to verify the compactness (aka, property of finite generated) of an object in finite dimension, one just need to take and compare the basis.