内切圆切点到高线足的距离

hbghlyj

C. V. Durell, A. Robson - Advanced Trigonometry
(page 22) Evercise I. g.
10. $P$是$BC$上的内切圆切点, $D$是$BC$上的高线足, 证明
$$P D=4 R \sin \frac{B}{2} \sin \frac{C}{2} \sin \frac{\abs{B-C}}{2}$$
11. $O$是外心, $I$是内心, $R,r$为外接圆,内切圆半径. 证明$$\S{O A I}=\frac{R^{2} r}{a}\abs{\cos B - \cos C}$$
12. 高线$AD$与内切圆的交角为$$\cos ^{-1}\left(\sin \frac{B-C}{2} \operatorname{cosec} \frac{A}{2}\right)$$
13. $r,r_1,R$为内切圆,$A$-旁切圆,外接圆半径. 若$\frac{r}{2}=\frac{r_{1}}{12}=\frac{R}{5}$, 则$\triangle ABC$为直角三角形.

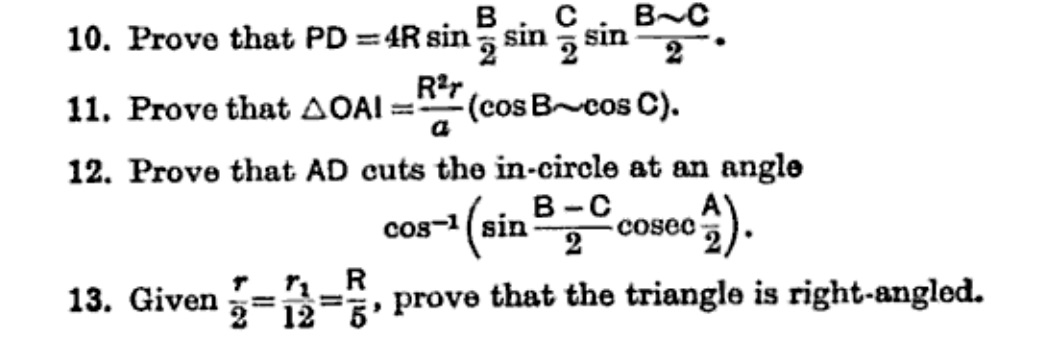
hbghlyj

根据10
高线$AD$与内切圆的交角为$$\cos ^{-1}\frac{PD}{r}=\cos ^{-1}\frac{4 R \sin \frac{B}{2} \sin \frac{C}{2} \sin \frac{\abs{B-C}}{2}}{4R\sin\frac A2\sin\frac B2\sin\frac C2}=\cos ^{-1}\left(\sin \frac{B-C}{2} \operatorname{cosec} \frac{A}{2}\right)$$

intouch、foot参见geometry.asy

hbghlyj

\begin{align*}PD&=\abs{BP-BD}\\&=\abs{\frac{a-b+c}2-c\cos B}
\\&=\abs{\frac{2R (\sin (B+C)-\sin (B)+\sin (C))}2-2 R \sin (C)\cos (B) }\\&=4 R \sin \left(\frac{B}{2}\right) \sin \left(\frac{C}{2}\right) \sin \left(\frac{\abs{B-C}}{2}\right)
\end{align*}

hbghlyj

由 $\angle OAI=\frac{\abs{B-C}}2$ 得
$$\S{O A I}=\frac12AO\cdot AI\cdot\sin\angle OAI=\frac12R\frac{r}{\sin\frac A2}\sin\frac{\abs{B-C}}2$$
由 $\abs{\cos B - \cos C}=2\sin{\abs{B-C}\over2}\cos\frac A2$ 得
$$=\frac12R\frac{r}{\sin\frac A2}{\abs{\cos B - \cos C}\over2\cos\frac A2}=\frac12R\frac{r}{\sin A}\abs{\cos B - \cos C}$$
由 $\frac{2R}{a}=\frac1{\sin A}$ 得
$$=\frac{R^2r}a\abs{\cos B - \cos C}$$

hbghlyj

只需证明 $2R+r=r_1\Leftrightarrow A=\frac\pi2$
事实上, 我们有恒等式 $r_1-r=2R(1-\cos A)$ 见MSE
$$r_1-r=4R\sin \frac A2 \cos \frac B2 \cos \frac C2-4R\sin \frac A2 \sin \frac B2 \sin \frac C2=4R\sin\frac A2\cos\frac{B+C}2=4R\sin^2\frac A2=2R(1-\cos A)$$

hbghlyj

hbghlyj 发表于 2023-3-3 22:19
事实上, 我们有恒等式 $r_1-r=2R(1-\cos A)$ 见MSE

incenter-excenter lemma (Fact5.pdf | MSE | AOPS) 以$IJ$为直径的圆通过$B,C$且圆心$M$为外接圆$\overparen{BC}$中点.

对$\triangle ABM$使用正弦定理$BM=2R\sin\frac A2\implies IJ=4R\sin\frac A2$
$$r_1=AJ\sin\frac A2,r=AI\sin\frac A2\implies$$
$$r_1-r=IJ\sin\frac A2=4R\sin^2\frac A2$$