|
|
线段 $A_1A_2,B_1B_2$ 的垂直平分线的交点 $P$ 是平面位移的instant center。
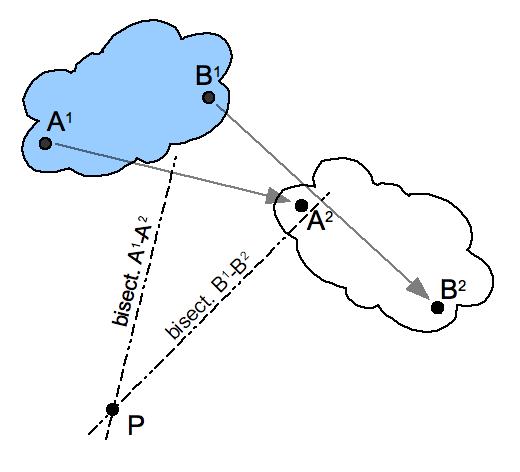
瞬间中心 $ \left(P_{x},P_{y}\right) $ 的代数构造如下:
$ A^{1}A^{2} $ 的中点的坐标$$ A_{x}^{m}={\frac {1}{2}}\left(A_{x}^{1}+A_{x}^{2}\right);\quad A_{y}^{m}={\frac {1}{2}}\left(A_{y}^{1}+A_{y}^{2}\right), $$
$ B^{1}B^{2} $ 的中点的坐标
$$ B_{x}^{m}={\frac {1}{2}}\left(B_{x}^{1}+B_{x}^{2}\right);\quad B_{y}^{m}={\frac {1}{2}}\left(B_{y}^{1}+B_{y}^{2}\right). $$
$\vv{A^{1}A^{2}}$ 和 $\vv{B^{1}B^{2}}$ 相对于水平方向逆时针测量的角度为
$$ \tan \tau _{A}={\frac {A_{y}^{2}-A_{y}^{1}}{A_{x}^{2}-A_{x}^{1}}},\quad \tan \tau _{B}={\frac {B_{y}^{2}-B_{y}^{1}}{B_{x}^{2}-B_{x}^{1}}}, $$
取 $\tan$ 的正确分支。设旋转的中心$\left(P_{x},P_{y}\right)$到两个中点的距离为$d_{A}$和$d_{B}$。假设顺时针旋转(否则切换$\pi/2$的符号):
$$ {\begin{aligned}P_{x}&=A_{x}^{m}+d_{A}\cos \left(\tau _{A}-{\frac {\pi }{2}}\right)\\&=B_{x}^{m}+d_{B}\cos \left(\tau _{B}-{\frac {\pi }{2}}\right);\\P_{y}&=A_{y}^{m}+d_{A}\sin \left(\tau _{A}-{\frac {\pi }{2}}\right)\\&=B_{y}^{m}+d_{B}\sin \left(\tau _{B}-{\frac {\pi }{2}}\right).\end{aligned}} $$
将其重写为具有 4 个未知数(两个距离 $d$ 和中心 $P$ 的两个坐标)的 4×4 非齐次线性方程组:
$$ {\begin{pmatrix}1&0&-\sin \tau _{A}&0\\1&0&0&-\sin \tau _{B}\\0&1&\cos \tau _{A}&0\\0&1&0&\cos \tau _{B}\end{pmatrix}}{\begin{pmatrix}P_{x}\\P_{y}\\d_{A}\\d_{B}\end{pmatrix}}={\begin{pmatrix}A_{x}^{m}\\B_{x}^{m}\\A_{y}^{m}\\B_{y}^{m}\end{pmatrix}}. $$
瞬间中心的坐标是解向量的前两个分量
$${\begin{pmatrix}P_{x}\\P_{y}\\d_{A}\\d_{B}\end{pmatrix}}={\frac {1}{\sin \left(\tau _{A}-\tau _{B}\right)}}{\begin{pmatrix}\left(B_{y}^{m}-A_{y}^{m}\right)\sin \tau _{A}\sin \tau _{B}+B_{x}^{m}\sin \tau _{A}\cos \tau _{B}-A_{x}^{m}\cos \tau _{A}\sin \tau _{B}\\\left(A_{x}^{m}-B_{x}^{m}\right)\cos \tau _{A}\cos \tau _{B}+A_{y}^{m}\sin \tau _{A}\cos \tau _{B}-B_{y}^{m}\cos \tau _{A}\sin \tau _{B}\\\left(B_{x}^{m}-A_{x}^{m}\right)\cos \tau _{B}+\left(B_{y}^{m}-A_{y}^{m}\right)\sin \tau _{B}\\\left(B_{x}^{m}-A_{x}^{m}\right)\cos \tau _{A}+\left(B_{y}^{m}-A_{y}^{m}\right)\sin \tau _{A}\\\end{pmatrix}}.$$ |
|