椭圆上一点P,求离心率

realnumber

椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1,a>b>0$上一点P(不是顶点),I为三角形$PF_1F_2$内心,$F_1,F_2$为两焦点,
若$k_1=\frac{3}{2}k_2$($k_1$为OP斜率,$k_2$为OI斜率),求这个椭圆的离心率.

realnumber

大概完成了$e=0.5$
P($x_0,y_0$),$PF_1=a+ex_0,PF_2=a-ex_0$由内角平分线性质解得PI与X轴交点($e^2x_0,0$),再次用内角平分线性质I($ex_0,\frac{ey_0}{1+e}$)

kuing

几何味道这么浓，来个纯平几解法吧。

先抛开椭圆，如下图：

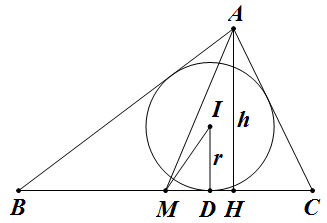
图中 `M` 为 `BC` 中点，高 `AH=h`，记三边长为 `a`, `b`, `c`（不是椭圆的 `a`, `b`, `c`），由面积公式有
\[r(a+b+c)=2S=ah\riff\frac hr=\frac{a+b+c}a,\]
不妨设 `AB>AC`，则易知
\[MD=\frac{BD-CD}2=\frac{AB-AC}2=\frac{c-b}2,\]
由勾股定理有
\begin{align*}
c^2-b^2&=BH^2+h^2-(CH^2+h^2)\\
&=(BH+CH)(BH-CH)\\
&=a\cdot2MH,
\end{align*}
得到
\[MH=\frac{c^2-b^2}{2a}=\frac{b+c}a\cdot\frac{c-b}2=\frac{b+c}a\cdot MD,\]
所以
\[\frac{\tan\angle AMH}{\tan\angle IMD}=\frac hr\cdot\frac{MD}{MH}=\frac{a+b+c}a\cdot\frac a{b+c}=\frac a{b+c}+1.\]

回到原题，就是
\[\frac{k_1}{k_2}=\frac{F_1F_2}{PF_1+PF_2}+1=e+1.\]