|
|
Last edited by hejoseph 2023-3-26 20:43
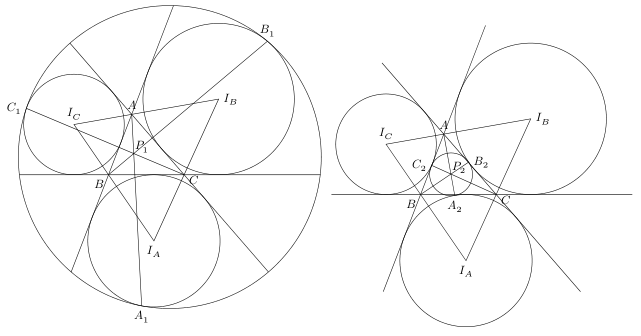
设$\triangle ABC$中$BC=a$,$CA=b$,$AB=c$,$p$是半周长,$R$是外接圆半径,$S$是面积,$\triangle ABC$与点$A$、$B$、$C$相对的旁切圆分别是$\odot I_A$、$\odot I_B$、$\odot I_C$。$\odot O_1$与$\odot I_A$、$\odot I_B$、$\odot I_C$均内切,切点分别是$A_1$、$B_1$、$C_1$;$\odot O_2$与$\odot I_A$、$\odot I_B$、$\odot I_C$均外切,切点分别是$A_2$、$B_2$、$C_2$。有如下结论:
(1) $\odot O_1$、$\odot O_2$的半径分别是$r_1$、$r_2$,则
\[
r_1=\frac{(a+b)(a+c)(b+c)-abc}{8S},r_2=\frac{abc}{8S}=\frac{R}{2};
\]
(2)令
\begin{align*}
f_1(x,y,z)&=-x^3(y+z)^2-x^2(y+z)(y^2+z^2)+2xyz(y^2+z^2)+(x+y+z)(x^4+z^4),\\
f_2(x,y,z)&=x^2(y^2+z^2)-(y^2-z^2)^2,
\end{align*}
点$O_1$、$O_2$的重心坐标分别是
\[
\left(\frac{af_1(a,b,c)}{32bcS^2},\frac{bf_1(b,c,a)}{32caS^2},\frac{cf_1(c,a,b)}{32abS^2}\right)、\left(\frac{f_2(a,b,c)}{32S^2},\frac{f_2(b,c,a)}{32S^2},\frac{f_2(c,a,b)}{32S^2}\right),
\]
且
\[
O_1O_2=\frac{(a+b)(a+c)(b+c)}{8S}\sqrt{\frac{a^3+b^3+c^3+5abc-(a+b)(a+c)(b+c)}{abc}};
\]
(3)令
\begin{align*}
f_3(x,y,z)&=2x(y^2+z^2)+y^3+z^3-x^3-xyz,\\
f_4(x,y,z)&=x^3+x^2(y+z)-x(y^2+z^2)-(y+z)(y-z)^2+3xyz,
\end{align*}
则点$A_1$、$B_1$、$C_1$的重心坐标分别是
\begin{align*}
&\left(-\frac{a(a(b+c)+b^2+c^2)^2}{2bcf_3(a,b,c)},\frac{2bp(c+a)^2(p-c)}{caf_3(a,b,c)},\frac{2cp(a+b)^2(p-b)}{abf_3(a,b,c)}\right)、\\
&\left(\frac{2ap(b+c)^2(p-c)}{bcf_3(b,c,a)},-\frac{b(b(c+a)+c^2+a^2)^2}{2caf_3(b,c,a)},\frac{2cp(a+b)^2(p-a)}{abf_3(b,c,a)}\right)、\\
&\left(\frac{2ap(b+c)^2(p-b)}{bcf_3(c,a,b)},\frac{2bp(c+a)^2(p-a)}{caf_3(c,a,b)},-\frac{c(c(a+b)+a^2+b^2)^2}{2abf_3(c,a,b)}\right),
\end{align*}
点$A_2$、$B_2$、$C_2$的重心坐标分别是
\begin{align*}
&\left(-\frac{p(b-c)^2}{f_4(a,b,c)},\frac{(a+c)^2(p-c)}{f_4(a,b,c)},\frac{(a+b)^2(p-b)}{f_4(a,b,c)}\right)、\\
&\left(\frac{(b+c)^2(p-c)}{f_4(b,c,a)},-\frac{p(c-a)^2}{f_4(b,c,a)},\frac{(b+a)^2(p-a)}{f_4(b,c,a)}\right)、\\
&\left(\frac{(c+b)^2(p-b)}{f_4(c,a,b)},\frac{(c+a)^2(p-a)}{f_4(c,a,b)},-\frac{p(a-b)^2}{f_4(c,a,b)}\right);
\end{align*}
(4)$AA_1$、$BB_1$、$CC_1$相交于同一点$P_1$,$AA_2$、$BB_2$、$CC_2$相交于同一点$P_2$,令
\begin{align*}
k_1&=a^3+b^3+c^3+3abc,\\
k_2&=(a+b)(a+c)(b+c)-(a^3+b^3+c^3+3abc),\\
k_3&=(a^2+b^2)(a^2+c^2)(b^2+c^2)+ab(a^4+b^4)+ac(a^4+c^4)+bc(b^4+c^4)-(a^3+b^3+c^3)^2-5a^2b^2c^2,
\end{align*}
则点$P_1$、$P_2$的重心坐标分别是
\begin{align*}
&\left(\frac{2a(b+c)^2(p-b)(p-c)}{bck_1},\frac{2b(c+a)^2(p-c)(p-a)}{cak_1},\frac{2c(a+b)^2(p-a)(p-b)}{abk_1}\right)、\\
&\left(\frac{(b+c)^2(p-b)(p-c)}{pk_2},\frac{(c+a)^2(p-c)(p-a)}{pk_2},\frac{(a+b)^2(p-a)(p-b)}{pk_2}\right),
\end{align*}
且
\[
P_1P_2=\frac{4S^2(a+b)(a+c)(b+c)}{pk_1k_2}\sqrt{\frac{k_3}{2abcp}}。
\] |
|