不相交曲线之间的最短距离

TSC999

TSC999

此题，网上搜了一下方法，解法如下：

第一步，求出 \(y=f(x)\) 形式的椭圆方程和双曲线方程：

第二步，用计算软件 mathematica 求两处的最短距离：

第三步，画图验证一下：

结论： 最短距离有两处，左上那处是  AB=0.108534，此时椭圆上的横坐标为 x1=-0.215242，

纵坐标为 y1=0.25558。双曲线上的横坐标为 x2=-0.289764，纵坐标为  y2= 0.33449。

另一处最短距离是 CD=0.281933，此时椭圆上的横坐标为  x1=0.320571，纵坐标为 y2=-0.139034，

双曲线上的横坐标为 x2=0.544245，纵坐标为 y2= -0.310663。

TSC999

这个方法是网上搜来的。有没有问题？有没有更好的方法？

uk702

如果只要粗略的数据，Geogebra 作图软件可以用如下方式操作：

f: x² - x y + y² = 1 / 6
g: x² - 6x y + y - 1 = 0

// 打点的数目
n = 5

// 以路径参数 i 作为间隔参数，对图形 f 打 n 个点
序列(描点(f, i), i, 0, 1, 1 / n)

// 对于每个打点，分别找到图形 g 上与这个打点对应的最近点
序列(最近点(g, 描点(f, i)), i, 0, 1, 1 / n)

// 分别显示每个打点到图形 g 上与这个打点对应的最近点的距离
// text(序列(距离(最近点(g, 描点(f, i)), 描点(f, i)), i, 0, 1, 1 / n))

// 建立两个个序列，分别保存每个打点和相应与g的最小距离，然后根据最小距离找到相应的打点序号
l1=序列(描点(f, i), i, 0, 1, 1 / n)
s2=序列(距离(最近点(g, 描点(f, i)), 描点(f, i)), i, 0, 1, 1 / n)
b = 最小值(s2)
i = 索引(b, s2)
D = l1(i)
E = l2(i)
l = 线段(D, E)

text(l)

uk702

如果要限定下半椭圆，就要指定路径的参数范围。

kuing

设
\begin{align*}
F(x,y)&=x^2-xy+y^2-\frac16,\\
G(x,y)&=x^2-6xy+y-1,
\end{align*}
用 `F_x` 表示 `F` 对 `x` 的偏导数，设点 `(x_1,y_1)`, `(x_2,y_2)` 分别在 `F=0` 和 `G=0` 上，则这两点处的切向量分别为
\begin{align*}
\vec u&=\bigl(F_y(x_1,y_1),-F_x(x_1,y_1)\bigr),\\
\vec v&=\bigl(G_y(x_2,y_2),-G_x(x_2,y_2)\bigr),
\end{align*}
在两点距离取极值时，必定是以上两切向量均与两点连线垂直，因此有方程组
\[\led
\vec u\cdot(x_1-x_2,y_1-y_2)&=0,\\
\vec v\cdot(x_1-x_2,y_1-y_2)&=0,\\
F(x_1,y_1)&=0,\\
G(x_2,y_2)&=0,
\endled\]
这个方程组最终毫无意外地涉及四次方程，无简单解，只能开软件求近似值。

mma 代码：

1. F[x_, y_] = x^2 - x y + y^2 - 1/6;
2. G[x_, y_] = x^2 - 6 x y + y - 1;
3. u[x_, y_] = {D[F[x, y], y], -D[F[x, y], x]};(*切向量*)
4. v[x_, y_] = {D[G[x, y], y], -D[G[x, y], x]};
5. {u[x1, y1].{x1 - x2, y1 - y2} == 0, v[x2, y2].{x1 - x2, y1 - y2} == 0,
6.   F[x1, y1] == 0, G[x2, y2] == 0}

Copy the Code

算出的方程组是：

1. {(x1 - x2) (-x1 + 2 y1) + (-2 x1 + y1) (y1 - y2) ==
2.   0, (1 - 6 x2) (x1 - x2) + (y1 - y2) (-2 x2 + 6 y2) ==
3.   0, -(1/6) + x1^2 - x1 y1 + y1^2 == 0, -1 + x2^2 + y2 - 6 x2 y2 == 0}

Copy the Code

然后用 NSolve 来解它，给出很多解，只有四组是实数，我将它们分别记为：

1. j1 = {y2 -> -0.4374599920708491`, x1 -> -0.4072004736133994`,
2.    y1 -> 0.00208762716062023`, x2 -> 0.46520298782443953`};
3. j2 = {y2 -> 0.30012503474685104`, x1 -> 0.1665557500174892`,
4.    y1 -> -0.2986397250946714`, x2 -> -0.3286693593934353`};
5. j3 = {y2 -> 0.3344924728723728`, x1 -> -0.21524153403239277`,
6.    y1 -> 0.25558713238468383`, x2 -> -0.2897644214120727`};
7. j4 = {y2 -> -0.3106629554665209`, x1 -> 0.32057074109792955`,
8.    y1 -> -0.13903463651810666`, x2 -> 0.5442449235400255`};

Copy the Code

然后在图上把它们给标出来：

1. Show[ContourPlot[{F[x, y] == 0, G[x, y] == 0}, {x, -1, 1}, {y, -1,
2.    1}], Graphics[{Red, Point[{{x1, y1}, {x2, y2}}] /. j1,
3.    Line[{{x1, y1}, {x2, y2}}] /. j1,
4.    Darker[Green], Point[{{x1, y1}, {x2, y2}}] /. j2,
5.    Line[{{x1, y1}, {x2, y2}}] /. j2,
6.    Blue, Point[{{x1, y1}, {x2, y2}}] /. j3,
7.    Line[{{x1, y1}, {x2, y2}}] /. j3,
8.    Purple, Point[{{x1, y1}, {x2, y2}}] /. j4,
9.    Line[{{x1, y1}, {x2, y2}}] /. j4}]]

Copy the Code

输出：

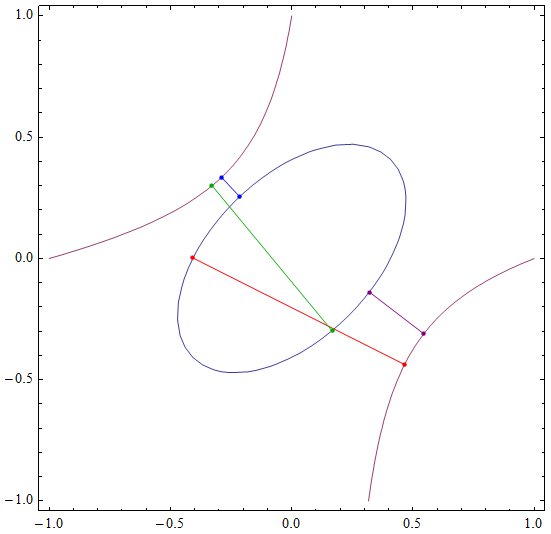
那前两组就该舍掉了，最后用

1. Norm[{x1 - x2, y1 - y2}] /. j3
2. Norm[{x1 - x2, y1 - y2}] /. j4

Copy the Code

得到最短的蓝线和另一支上的紫线长分别为
0.108534
0.281933