|
|
Last edited by TSC999 2023-3-27 16:18 梅涅劳斯定理是针对【完全四边形】的,见图 (1)。梅涅劳斯定理如何记忆? 即书写比例式时如何避免写错?有一个诀窍:
就是下面提出的【完全四边形环游规则】。
另外,梅氏定理也可用于【风筝四边形】,见图(2)。因为它可以看作是三个不同的完全四边形 (ECABDFE,ABFHECA,DBCHEFD) 组合而成的,所以可以对每一个完全四边形使用梅氏定理。
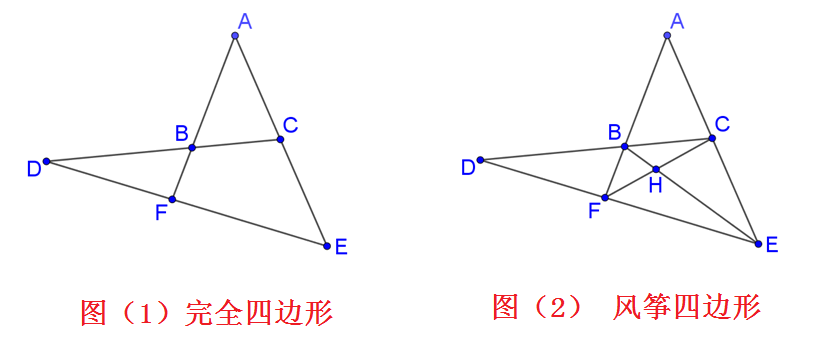
在上面两个图中,我们可以把图中的每一条线段看成是一条公路,线上的点看作城市,无论图(1)或图(2),每一条公路上都恰好有三个城市,在图(1)中共有 A、B、C、D、E、F 六个城市,共有四条公路 AE、AF、DE、DC 把它们连接起来。在(2)中共有 A、B、C、D、E、F、H 七个城市,共有六条公路 AE、AF、DE、DC、BE、CF 把它们连接起来。
假定您在其中一个城市居住,现在您从居住地开车出发,打算经过三条公路周游某些城市后,再回到居住地。
游历路线可以有许多种,但必须遵守一个规则,就是在每一条公路上行驶时,必须游览过这条公路上的三个城市,然后才能换行到另一条公路上去。例如对于图(1),您从居住地 A 城出发,先驶上 AF 路。然后又可以有多种选择 :
① 到达 B 城下车游览后,再继续行驶到 F 城游览,接下来可以行驶到 D 城游览后,不能立即换到另一条路上,因为还没有游览 E 城,所以要继续从 D 行驶到 E,途经 F 不停,因为 F 城已经游览过了。到达 E 城下车游览后,就要考虑回到出发地 A 了。
这时不能直接从 F 行驶到 A,因为 C 城还没有游览,于是先从 E 到 C 游览后,再从 C 回到 A。
把上述游览过程记录下来,就是 A → B → F → D → E → C → A。写成比例式就是 \(\frac{AB}{BF}\frac{FD}{DE}\frac{EC}{CA}=1\),也就是按照梅涅劳斯定理,这三个比例之积等于 1。
② 选择 A → B → F → E → D → C → B → F → A。写成比例式就是\(\frac{AB}{BF}\frac{FE}{ED}\frac{DC}{CB}\frac{BF}{FA}=1\),如果分子分母消去 BF,就有\(\frac{AB}{FA}\frac{FE}{ED}\frac{DC}{CB}=1\)
③ 选择 A → F → B → D → C → E → A。写成比例式就是 \(\frac{AF}{FB}\frac{BD}{DC}\frac{CE}{EA}=1\)。
同样,如果从除 A 以外的其他城市出发,就可以写出许许多多的别的比例式。例如从 B 出发,可以写出: \(\frac{BF}{FA}\frac{AE}{EC}\frac{CD}{DB}=1\)。
对于风筝四边形,使用环游规则,从 F 出发,可以选择路线 F → D → E → H → B → D → C → E → A → B → F。
写成比例式就是 \(\frac{FD}{DE}\frac{EH}{HB}\frac{BD}{DC}\frac{CE}{EA}\frac{AB}{BF}=1\)。为了证明这个比例式确实是成立的,证明如下:

|
|