|
|
|
4.用中心投影法证明:
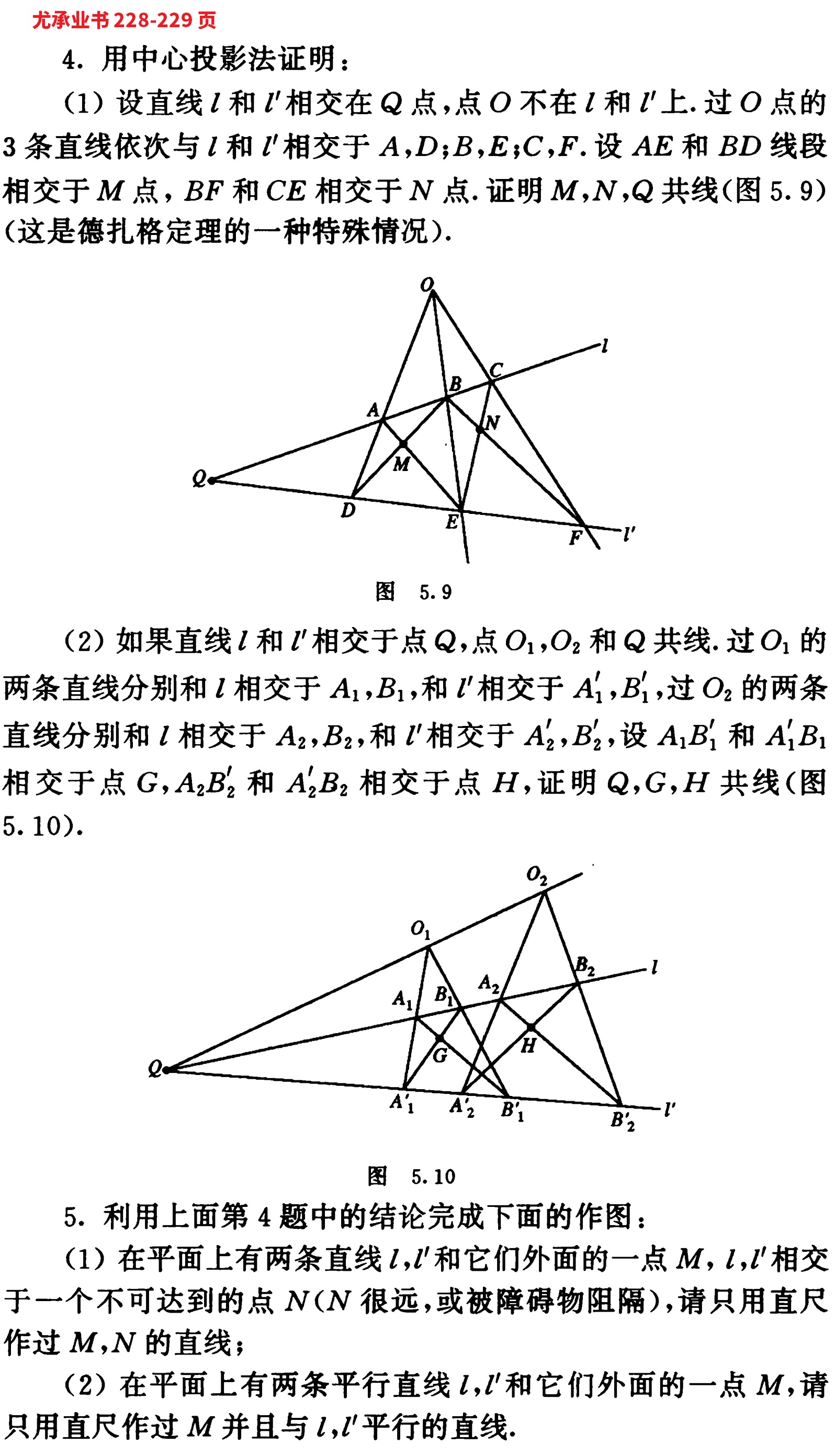
(1) 设直线 $l$ 和 $l^{\prime}$ 相交在 $Q$ 点, 点 $O$ 不在 $l$ 和 $l^{\prime}$ 上. 过 $O$ 点的 3 条直线依次与 $l$ 和 $l^{\prime}$ 相交于 $A, D ; B, E ; C, F$. 设 $A E$ 和 $B D$ 线段相交于 $M$ 点, $B F$ 和 $C E$ 相交于 $N$ 点. 证明 $M, N, Q$ 共线(图 5.9) (这是德扎格定理的一种特殊情况).
(2) 如果直线 $l$ 和 $l^{\prime}$ 相交于点 $Q$, 点 $O_1, O_2$ 和 $Q$ 共线. 过 $O_1$ 的两条直线分别和 $l$ 相交于 $A_1, B_1$, 和 $l^{\prime}$ 相交于 $A_1^{\prime}, B_1^{\prime}$, 过 $O_2$ 的两条直线分别和 $l$ 相交于 $A_2, B_2$, 和 $l^{\prime}$ 相交于 $A_2^{\prime}, B_2^{\prime}$, 设 $A_1 B_1^{\prime}$ 和 $A_1^{\prime} B_1$ 相交于点 $G$, $A_2 B_2^{\prime}$ 和 $A_2^{\prime} B_2$ 相交于点 $H$, 证明 $Q, G, H$ 共线 (图 5.10).
5.利用上面第4题中的结论完成下面的作图:
(1)在平面上有两条直线$l,l'$和它们外面的一点$M$, $l,l'$相交于一个不可达到的点$N$($N$很远,或被障碍物阻隔),请只用直尺作过$M,N$的直线;
(2)在平面上有两条平行直线$l,l'$,和它们外面的一点$M$,请只用直尺作过$M$并且与$l,l'$平行的直线. |
|
|