射影变换将正方形映射到不连通区域

hbghlyj

见hw10补充题五
3) 一个三角形区域的像，一定还是一个三角形区域吗？
Planar Homography

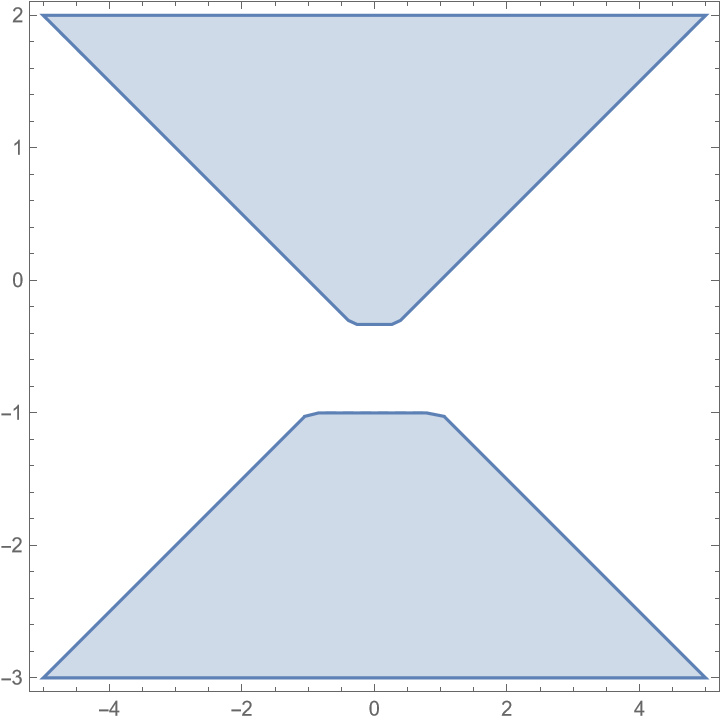
正方形区域$\{(x,y):\abs x\le1,\abs y\le1\}$经过射影变换$\left(
\begin{array}{cc|c}
1 & 0 & 0 \\
0 & 1 & 0 \\\hline
0 & -2 & 1 \\
\end{array}
\right)$变成什么?
根据定义写出$\begin{cases}x'=\frac{x}{1-2 y}\\
y'=\frac{y}{1-2 y}\end{cases}\implies\begin{cases}x=\frac{x'}{1+2y'}\\y=\frac{y'}{1+2y'}\end{cases}$
\begin{align*}
\abs x\le1&\iff \abs{x'}\le\abs{1+2y'}\\
\abs y\le1&\iff y'>-\frac13\vee y'<-1\end{align*}
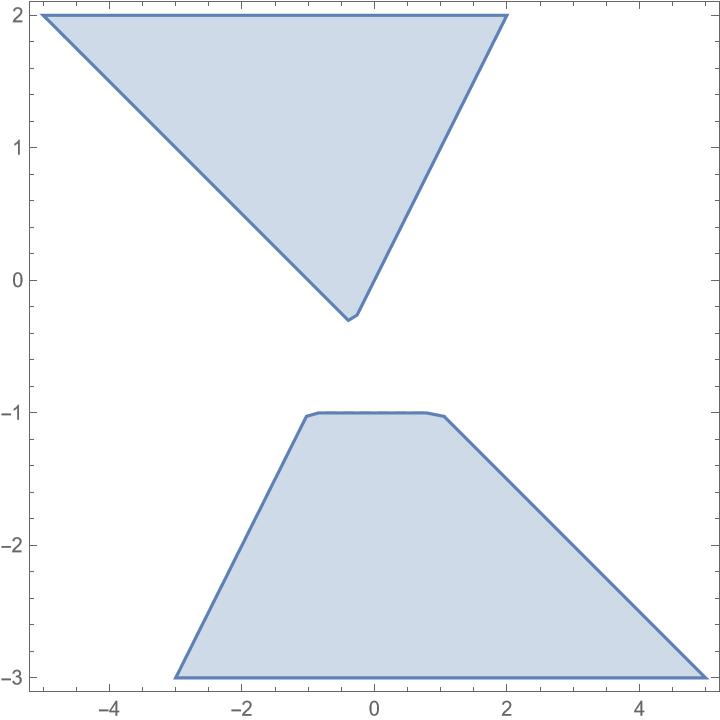
把三角形$\{(x,y):x\le y,\abs x\le1,\abs y\le1\}$变成什么?
\[x\le y\iff(y'-x')(1+2y')\ge0\]

RegionPlot[(y > -(1/3) || y < -1) && Abs[x] < Abs[1 + 2 y], {x, -5, 5}, {y, -3, 2}] Copy the Code
RegionPlot[(y > -(1/3) || y < -1) && Abs[x] < Abs[1 + 2 y] && (y - x) (1 + 2 y) > 0, {x, -5, 5}, {y, -3, 2}] Copy the Code

Czhang271828

应当在紧 Riemann 面 $\mathbb P_{\mathbb R}^2:=\{(X:Y:Z)\mid X,Y,Z\in \mathbb R^3\}$ 上研究这类问题($\overline{\mathbb C}$ 想来也不大适合), 这里两张图都是对角线在图形外的凹四边形.

hbghlyj

Czhang271828 发表于 2023-3-27 05:57
这里两张图都是对角线在图形外的凹四边形

为什么是凹四边形呢?

Czhang271828

hbghlyj 发表于 2023-5-14 08:54
为什么是凹四边形呢?

凸四边形上选取一点绕一圈, 经历四次右转或四次左转, 凹四边形则是两次左转两次右转.

选定一楼第一张图的 $(0,-1)$ 往 $x_+$ 方向绕圈, 那么
[Step 1] 右转, 走到右下方无穷远处
[Step 2] 经该方向的无穷远点到达左上方无穷远处,
[Step 3] 走到下一个拐点后左转
[Step 4] 走到下一个拐点后左转
[Step 5] 走到右上方无穷远处,
[Step 6] 经该方向无穷远处到达左下方无穷远处,
[Step 7] 走到下一个拐点后左转, 继而回到出发点.

虽然 $\mathbb P_{\mathbb R}^2$ 是不可定向的, 但一楼的四边形所在的区域是 $\mathbb P_{\mathbb R}^2$ 中可定向的子流形. 容易发现 $\mathbb P_{\mathbb R}^2\setminus \overline{\mathbb R}$ 是个可定向单连通流形, 同胚与 $\mathbb R^2$.