费马螺线的极坐标方程:$r=\pm a{\sqrt {\varphi }},\quad \varphi \geq 0$
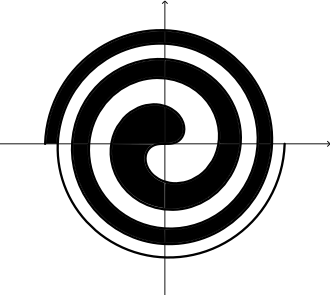
费马螺线将平面分为黑,白两部分:
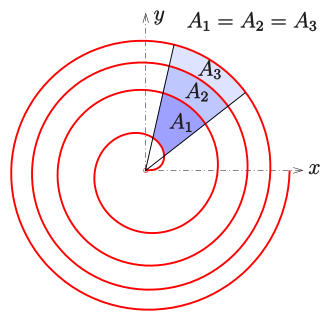
费马螺线相邻的弧之间的面积相等.
证明在两点$(r,\varphi_1)$与$(r,\varphi_2)$之间的扇形面积为
\begin{aligned}{\underline {A}}&={\frac {1}{2}}\int _{\varphi _{1}}^{\varphi _{2}}r(\varphi )^{2}\,d\varphi \\&={\frac {1}{2}}\int _{\varphi _{1}}^{\varphi _{2}}a^{2}\varphi \,d\varphi \\&={\frac {a^{2}}{4}}\left(\varphi _{2}^{2}-\varphi _{1}^{2}\right)\\&={\frac {a^{2}}{4}}\left(\varphi _{2}+\varphi _{1}\right)\left(\varphi _{2}-\varphi _{1}\right)\end{aligned}增加2π之后变为${\overline {A}}={\frac {a^{2}}{4}}\left(\varphi _{2}+\varphi _{1}+4\pi \right)\left(\varphi _{2}-\varphi _{1}\right)={\underline {A}}+a^{2}\pi \left(\varphi _{2}-\varphi _{1}\right)$
所以相邻弧之间的面积$A=a^{2}\pi \left(\varphi _{2}-\varphi _{1}\right)$只取决于弧关于原点的张角.
费马螺线与黄金分割率:
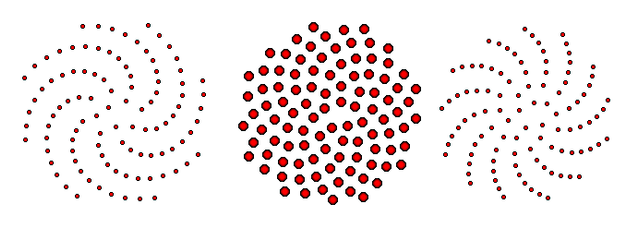Vogel模型产生的小花图案(中央图片).另外两张图片显示了角度不等于黄金分割角时的模式. 在圆盘叶序中,如向日葵和菊花,螺旋线的网状结构以斐波那契数列出现,因为离散度(单个螺旋排列的连续角)接近黄金分割率.螺旋线的形状取决于顺序生成的元素的增长.在成熟盘叶序中,当所有元素大小相同时,螺旋线的形状理想为费马螺线.这是因为费马螺线以相等的圈数穿过相等的环隙.由 h. Vogel 在1979年提出的完整模型是
\begin{aligned}r&=c{\sqrt {n}},\\\theta &=n\times 137.508°,\end{aligned}其中\(θ\)是角度,\(r\)是距离中心的半径或距离,\(n\)是小花的指数,\(c\)是一个恒定的比,而137.508°=360°×(1-0.618)是黄金角. | 
