三角形角B和角C的平分线交对边于D,E,DE交外接圆于F,求FA长

TSC999

已知三角形 ABC 的三边长度为 \(a，b，c\)，角 B 和角 C 的平分线交对边于 D、E，DE 的延长线交三角形ABC 的外接圆于 F 和 F1。

求 FA、FB、F1A、F1C 的长度（都用 \(a，b，c\) 的长度表示）。

TSC999

已知有下面这几个关系式，但似乎还不足以解出 \(x\) 和 \(y\) 与 \(a，b，c\) 的关系。

hejoseph

\begin{align*}
FA^2&=\frac{bc\left(a^2(b+c)+2a(b^2-bc+c^2)+(b+c)(b-c)^2-(a+b+c)(b-c)\sqrt{a^2+2a(b+c)+(b-c)^2}\right)}{2\left(a^3+a^2(b+c)-a(b^2-3bc+c^2)-(b+c)(b-c)^2\right)}\\
FB^2&=\frac{ac\left(a^3+a^2(2b+c)+a(b^2+2bc-c^2)-c(b-c)^2-(a+b-c)(a+c)\sqrt{a^2+2a(b+c)+(b-c)^2}\right)}{2\left(a^3+a^2(b+c)-a(b^2-3bc+c^2)-(b+c)(b-c)^2\right)}\\
F_1A^2&=\frac{bc\left(a^2(b+c)+2a(b^2-bc+c^2)+(b+c)(b-c)^2-(a+b+c)(c-b)\sqrt{a^2+2a(b+c)+(b-c)^2}\right)}{2\left(a^3+a^2(b+c)-a(b^2-3bc+c^2)-(b+c)(b-c)^2\right)}\\
F_1C^2&=\frac{ab\left(a^3+a^2(2c+b)+a(c^2+2bc-b^2)-b(b-c)^2-(a+c-b)(a+b)\sqrt{a^2+2a(b+c)+(b-c)^2}\right)}{2\left(a^3+a^2(b+c)-a(b^2-3bc+c^2)-(b+c)(b-c)^2\right)}
\end{align*}

hejoseph

直线 $FF_1$ 关于 $\triangle ABC$ 的重心坐标方程是
\[
\begin{vmatrix}
\alpha & \beta & \gamma \\
a & b & 0 \\
a & 0 & c
\end{vmatrix}=0
\]
$\triangle ABC$ 的外接圆关于 $\triangle ABC$ 的重心坐标方程是
\[
c^2\alpha\beta+b^2\alpha\gamma+a^2\beta\gamma=0
\]
标准重心坐标需要满足
\[
\alpha+\beta+\gamma=1
\]
由上面这三个方程组成的方程组解出 $(\alpha,\beta,\gamma)$ 就是点 $F$、$F_1$ 的标准重心坐标，然后用两点的重心坐标确定的距离公式就可以求两点距离了。
至于哪个解对应点 $F$ 和 $F_1$，用一下余弦定理计算 $\angle AFB$ 以及 $\angle AF_1C$ 的余弦值即可确定。

TSC999

这个题目的原意是要证明 \(\frac{1}{x}=\frac{1}{y}+\frac{1}{z}\) 以及
\(\frac{1}{x1}=\frac{1}{y1}+\frac{1}{z1}\)，这个能否证明呢？

另外，在 3# 楼中，给出了用三角形三边长度 \(a，b，c\) 来表示 \(x，y，x1，y1\) 的最简公式，而由\(z=\frac{bx+ay}{c}\) 虽然也能算出 \(z\)，但\(z\)的表达式并非最简：有没有用 \(a，b，c\) 来表示 \(z\) 和  \(z1\) 的最简公式呢？

hejoseph

TSC999 发表于 2023-4-10 19:15
这个题目的原意是要证明 \(\frac{1}{x}=\frac{1}{y}+\frac{1}{z}\) 以及
\(\frac{1}{x1}=\frac{1}{y1}+\f ...

\begin{align*}
FA^2&=\frac{bc\left(a^2(b+c)+2a(b^2-bc+c^2)+(b+c)(b-c)^2-(a+b+c)(b-c)\sqrt{a^2+2a(b+c)+(b-c)^2}\right)}{2\left(a^3+a^2(b+c)-a(b^2-3bc+c^2)-(b+c)(b-c)^2\right)}\\
FB^2&=\frac{ac\left(a^3+a^2(2b+c)+a(b^2+2bc-c^2)-c(b-c)^2-(a+b-c)(a+c)\sqrt{a^2+2a(b+c)+(b-c)^2}\right)}{2\left(a^3+a^2(b+c)-a(b^2-3bc+c^2)-(b+c)(b-c)^2\right)}\\
FC^2&=\frac{ab\left(a^3+a^2(b+2c)+a(c^2+2bc-b^2)-b(b-c)^2+(a-b+c)(a+b)\sqrt{a^2+2a(b+c)+(b-c)^2}\right)}{2\left(a^3+a^2(b+c)-a(b^2-3bc+c^2)-(b+c)(b-c)^2\right)}\\
F_1A^2&=\frac{bc\left(a^2(b+c)+2a(b^2-bc+c^2)+(b+c)(b-c)^2-(a+b+c)(c-b)\sqrt{a^2+2a(b+c)+(b-c)^2}\right)}{2\left(a^3+a^2(b+c)-a(b^2-3bc+c^2)-(b+c)(b-c)^2\right)}\\
F_1C^2&=\frac{ab\left(a^3+a^2(2c+b)+a(c^2+2bc-b^2)-b(b-c)^2-(a+c-b)(a+b)\sqrt{a^2+2a(b+c)+(b-c)^2}\right)}{2\left(a^3+a^2(b+c)-a(b^2-3bc+c^2)-(b+c)(b-c)^2\right)}\\
F_1B^2&=\frac{ac\left(a^3+a^2(c+2b)+a(b^2+2bc-c^2)-c(b-c)^2+(a-c+b)(a+c)\sqrt{a^2+2a(b+c)+(b-c)^2}\right)}{2\left(a^3+a^2(b+c)-a(b^2-3bc+c^2)-(b+c)(b-c)^2\right)}
\end{align*}

公式的形式很相似的。至于证明我没想过什么简便方法，既然得到长度了，直接两边平方验证一下是可以的。

TSC999

经检查，发现楼上 F1B 公式有一处笔误之处，改正后的公式如下：

TSC999

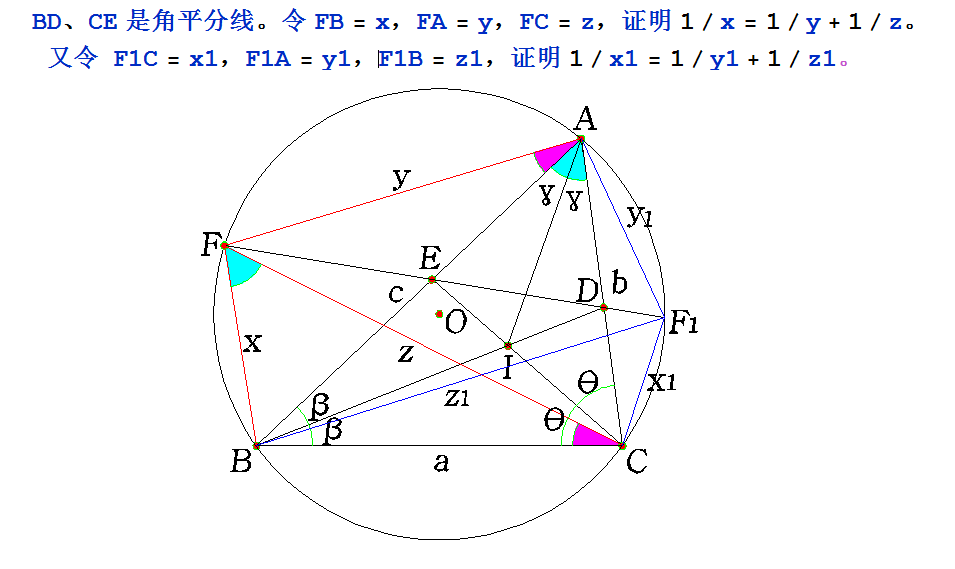
以下是【数学中国】网友 creasson 给出的用 MMA 写的证明程序。

1. Clear["Global`*"]; (*令 s=tanA/2, t=tanB/2, u=1/tan\[Angle]BAC*)
2. Print["根据构图，可直接引用此构图下的各点坐标如下(但 F 点的坐标最终尚取决于参变数 u 的取值)： "];
3. points = {B -> 0, C -> 1, A -> ((s + t) (1 - s t))/(s (1 - I t)^2),  pI -> (1 - s t)/(1 - I t), D -> (2 I (s^2 t + s (t^2 - 1) - t))/((t + I) (s^2 t - 2 s - t)),  pE -> ((t - I) (s t - 1))/((t + I) (s t + 1)), F -> (1 + I*(1 - s^2)/(2 s))/(1 - I u)}(*pI是内心的表示*)(*取值范围限定*)
4. cond = s > 0 && t > 0 && 1 - s t > 0;(*根据D,E,F共线得到u的方程：*)
5. uEQ = (Factor[ComplexExpand[Im[#]]] //
6.       Numerator) &@((D - F)/(D - pE) /. points);(*因D,E,F共线所以该式虚部的分子为零*)
7. Print["参数 u 应满足以下方程: "];
8. Print[uEQ, " = 0  -------①"];
9. Print["根据 F 点的位置确定参数 s、t、u 的取值范围如下: "];
10. cond = Reduce[Factor[ComplexExpand[Im[(F - B)/(A - B) /. points]]] > 0 &&  cond, {s, t, u}]
11. (*计算 FA,FB,FC的长度*)
12. Print["FA、FB、FC 的长度: "];
13. dists = FullSimplify[ComplexExpand[Abs[#]], Assumptions -> cond] & /@ ({F - A, F - B, F - C} /. points);
14. {FA -> dists[[1]], FB -> dists[[2]], FC -> dists[[3]]}
15. target = (1/dists[[2]] - 1/dists[[1]] - 1/dists[[3]]) // Factor;
16. Print["如果能证明下面这个式子等于零，则完成证明: "];
17. Print[target, "   -------②"];
18. Print["因为 ① 式等于零，而 ① 式的前两个因式不等于零，故第三个因式应为零。② 式分子中也有这个因式，所以 ② 式必为零，故命题 1/FB - 1/FA -1/FC = 0 成立。"]

Copy the Code

kuing

TSC999 发表于 2023-4-10 19:15
这个题目的原意是要证明 \(\frac{1}{x}=\frac{1}{y}+\frac{1}{z}\) 以及
\(\frac{1}{x1}=\frac{1}{y1}+\f ...

纯粹证 `1/x=1/y+1/z` 倒可以很简洁：

记 `\triangle ABC` 面积为 `S`，设 `DE=\lambda\cdot DF`，则有如下面积关系式
\begin{align*}
&\led
\S{AEC}&=\lambda\S{AFC},\\
(1-\lambda)\S{ADB}&=\lambda\S{AFB},\\
\S{BEC}&=\lambda\S{BFC}+(1-\lambda)\S{BDC}
\endled\\
\iff{}& \led
\frac b{a+b}S&=\lambda\cdot\frac12yz\sin B,\\
(1-\lambda)\frac c{a+c}S&=\lambda\cdot\frac12xy\sin C,\\
\frac a{a+b}S&=\lambda\cdot\frac12xz\sin A+(1-\lambda)\frac a{a+c}S
\endled\\
\iff{}& \led
\frac{abc}{a+b}&=\lambda yz,\\
(1-\lambda)\frac{abc}{a+c}&=\lambda xy,\\
\frac{abc}{a+b}&=\lambda xz+(1-\lambda)\frac{abc}{a+c},
\endled
\end{align*}
前两式代入后式即得
\[yz=xz+xy,\]
即得证。

TSC999

上图中，\(N\) 和 \(O\) 分别是三角形ABC的内心和外心，\(D、E\) 是三角形ABC 角平分线与对边的交点，DE 延长线交外接圆于 \(F\) 点。\(G\) 是 \(AC\) 弧的中点。作 \(HI // CF\) 并与 \(AF\) 交于 \(I\) 点。
如果能证明 \(FB = FI\) 或者 \(PI = PA\)，也可证明 \(\frac{1}{FB}=\frac{1}{FA}+\frac{1}{FC}\)。
不知怎样证明 \(FB = FI\) 或者 \(PI = PA\) ？

TSC999

9# 楼列出的下图面积关系，前两个 ①、② 都清楚明白，第 ③ 个关系式是怎么来的？想了半天也没弄懂，
哪位能给个详细的推导过程？

TSC999

噢，原来还有这么一个面积的定比分点公式。证明如下：

hbghlyj

TSC999 发表于 2023-4-17 15:08
噢，原来还有这么一个面积的定比分点公式。证明如下：

几何瑰宝 平面几何500名题暨1000条定理 (上) 沈文选，杨清桃 编著 page12-13