抛物线与双曲线相切于2个虚点

hbghlyj

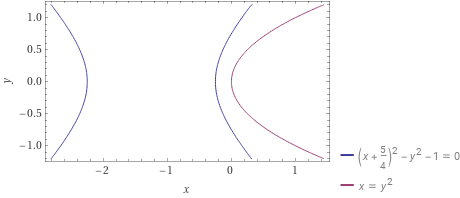
双曲线\begin{equation}\label1\left(x+\frac54\right)^2-y^2=1\end{equation}与抛物线\begin{equation}\label2x=y^2\end{equation}相切于2个虚点$(-\frac34,\pm\sqrt{-\frac34})$喔!
\eqref{1}对$x$求导得$\frac{dy}{dx} = {4 x + 5\over4 y}$ (4x+5)/(4y)/.{x->-3/4,y->Sqrt[-3/4]} 复制代码 \eqref{1}在点$(-\frac34,\sqrt{-\frac34})$的切线斜率为$-\frac{i}{\sqrt3}$	\eqref{2}对$x$求导得$\frac{dy}{dx} = \frac1{2 y}$ 1/(2y)/.{x->-3/4,y->Sqrt[-3/4]} 复制代码 \eqref{2}在点$(-\frac34,\sqrt{-\frac34})$的切线斜率为$-\frac{i}{\sqrt3}$

一般地,$\frac{\left(x+\frac{a^2+4 b^4}{4 b^2}\right)^2}{a^2}-\frac{y^2}{b^2}=1$与\eqref{2}相切于点$({a^2-4 b^4\over4 b^4},\pm\sqrt{a^2-4 b^4\over4 b^4})$.它们是虚的,当$a^2<4 b^4$ [\eqref{1}中$a=b=1$]