阿基米德三角形这个结论是否跟极点极线有关

hjfmhh

请问这个结论是否跟极点极线有关，怎么证明

Ly-lie

要用到熟知的小结论：$\angle HTG=\angle HFG=90^\circ$,这个应该不用多说，然后有$F,H,T,G$共圆，导角得$\triangle FHT\sim \triangle FGA$以及$\triangle FGT\sim \triangle FHB$,从而$\frac{HT}{GA}=\frac{FH}{FG}=\frac{BH}{TG}$

kuing

跟极点极线没啥关系，只是道简单的平几题。

首先根据 forum.php?mod=redirect&goto=findpost& … d=3441&pid=14170 中的命题，可知本题的 `G`, `T`, `F`, `H` 四点共圆：

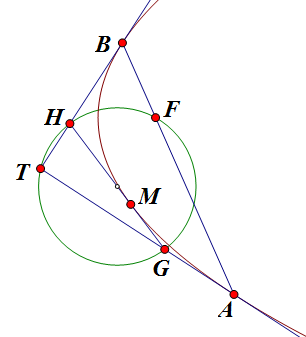
而由于 `AB` 过焦点，故 `TF\perp AB` 且 `\angle T` 为直角，因此 `GH` 是圆的直径。

此时抛物线可擦去，问题简化为以下初中几何题：

如下图（左），在 `\Rtt TAB` 中，`TF` 是斜边上的高，过 `T`, `F` 的圆交 `TA`, `TB` 于 `G`, `H`，求证：`TG\cdot TH=GA\cdot HB`。

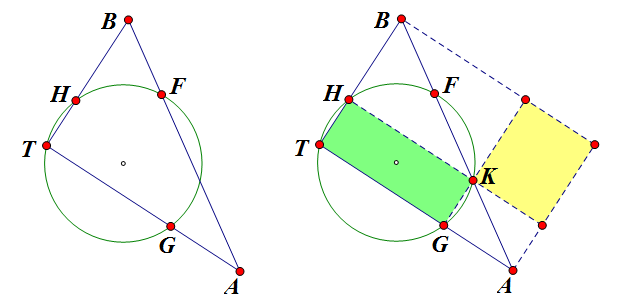
证明：设圆与 `AB` 的另一交点为 `K`，则 `TF\perp FK`，故 `TK` 也是圆的直径，因此 `TGKH` 为矩形，于是作如上图（右）的辅助线，显然黄色矩形面积 = 绿色矩形面积，即 `TG\cdot TH=GA\cdot HB`。

Ly-lie

楼主可以试试证明如下推广结论：抛物线任意外切线三角形的外接圆过焦点，且其垂心在准线上.

hjfmhh

Ly-lie 发表于 2023-4-24 14:44
要用到熟知的小结论：$\angle HTG=\angle HFG=90^\circ$,这个应该不用多说，然后有$F,H,T,G$共圆，导角得$\ ...

请问角HFG=90度怎么证的？谢谢

Ly-lie

hjfmhh 发表于 2023-4-24 20:18
请问角HFG=90度怎么证的？谢谢

见三楼提到的帖子，我跟三楼的证法差不多