一直线截两圆的弦相等 外公切线

hbghlyj

已知两圆$\Gamma_1$、$\Gamma_2$, 一条直线与$\odot\Gamma_1$交于A、B 两点，与O交于C、D两点(B、C在A、D之间), 与两圆的两条外公切线交于E、F两点。 求证：如果AB=CD，则EA=DF。

kuing

这样行不？：
不妨设 `AB=CD=1`，其余线长如图所设：

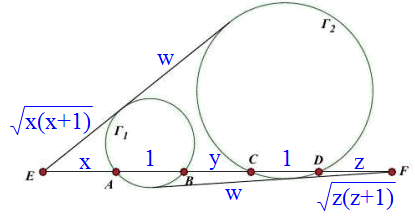
则有
\begin{align*}
(x+y+1)(x+y+2)&=\bigl(\sqrt{x(x+1)}+w\bigr)^2,\quad(1)\\
(z+y+1)(z+y+2)&=\bigl(\sqrt{z(z+1)}+w\bigr)^2,\quad(2)
\end{align*}
要证明 `x=z`，只需证明式 (1) 关于 `x` 的正数解是唯一的。

展开式 (1) 再移项平方化简最终可化为
\[4\bigl(w^2-(y+1)^2\bigr)x(x+y+2)-\bigl(w^2-(y+1)(y+2)\bigr)^2=0,\]
易证 `w>y+1`，故由韦达定理知，解 `x` 时它的两根之积 `\leqslant0`，不可能有两个正根，即得证。