regular tiling

hbghlyj

8.4. Special Kinds of Polyhedra: Regular Polyhedra and Fullerenes 8.4. Exercises
平面密铺 Euler公式

Imagine an infinite checkerboard▦ It is very like a regular map, except that it is not finite. It is an example of a regular tiling of the plane. Here is the definition of a regular tiling of a plane: an infinite set of polygons covering the plane, not overlapping except at edges, where each polygon is congruent to every other, and where each vertex has the same number of polygons meeting there. Although we have not proved this, regular tilings satisfy Eq. (8.12) but with $e$ set to infinity; that is,\begin{equation}\label1\frac1p + \frac1q = \frac12\end{equation}

每个面有相同数量的边 $p ≥ 3$，
每个顶点有相同的度数 $q ≥ 3$。
将$pf = qv = 2e$代入$v-e+f=2$得$\frac1p+\frac1q=\frac12+\frac1e$. 令$e\to\infty$得到\eqref{1}.
如何直接证明\eqref{1}呢? 在上面令$e\to\infty$感觉不太严格?

Czhang271828

"每个顶点具有相同的度数" 一句有误, 有些点没被铺满, 但此时已经考虑在极限情形了.

密铺当然不能用通常的收敛性描述, 应该加一个主值. 例如用长度为 $1$ 的区间密铺实数轴, 记 $a_k:=[k-0.5, k+0.5]$. 定义
\[
S_n=\{a_k\mid k\in \mathbb Z, |k|<n\}\cup \{ a_{2k}\mid  k\in \mathbb Z, |k|<n^n \}.
\]
那么以 $S_n$ 中所有区间决定的密铺序列 $\{P_n\}_{n\in \mathbb N_+}$ 随 $n\to +\infty$ 而密铺至整个平面. 但是 $P_n$ 中点与边的比例趋向 $2$, 而非密铺状态下的 $1$.

真正的密铺应该如何描述? 很简单, 存在固定的 $M>0$ 的使得对一切 $n$ 都有 (1) $S_n$ 铺满半径为 $n$ 的球, (2) $S_n$ 被半径为 $n+M$ 的球包围.

hbghlyj

正三角形镶嵌	正六边形镶嵌	正四边形镶嵌
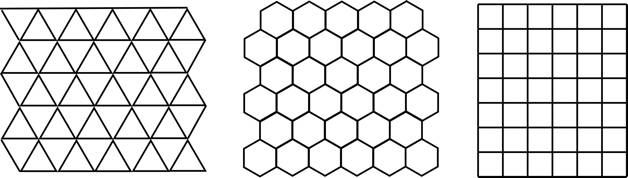
\begin{array}cp=3\\q=6\end{array}	\begin{array}cp=6\\q=3\end{array}	\begin{array}cp=4\\q=4\end{array}
对偶		自对偶

Mathematical Olympiad Dark Arts Chapter 7 page 87
The dual of the regular polyhedron with Schläfli symbol $\{a, b\}$ has the Schläfli symbol $\{b, a\}$.
For higher dimensions, we simply reflect the symbol.
The tetrahedron, with the palindromic Schläfli symbol $\{3, 3\}$, is thus self-dual, as is the square tiling with Schläfli symbol $\{4, 4\}$.
More generally, a simplex has Schläfli symbol $\{3, 3, 3, ..., 3, 3\}$ and a hypercubic tessellation has Schläfli symbol $\{4, 3, 3, ..., 3, 4\}$, both of which are palindromic.
For four-dimensional solids, the 4-simplex $\{3, 3, 3\}$ is not the only self-dual regular polychoron; we also have the 24-cell with Schläfli symbol $\{3, 4, 3\}$ (meaning that three octahedral cells are clustered around each edge)

---

（凸）正 $p$ 边形的 Schläfli 符号是 $\{p\}$。例如，正五边形由 $\{5\}$ 表示。

星形多边形（非凸正多边形）的 Schläfli 符号是 $\{p⁄q\}$，其中 $p$ 是顶点数，外接圆被顶点分成 $p$ 段小弧，$q$ 是星形每条边跨过的小弧数。例如，$\{5⁄2\}$ 代表五角星。
$\{np/nq\}$是$n$个$\{p/q\}$的复合

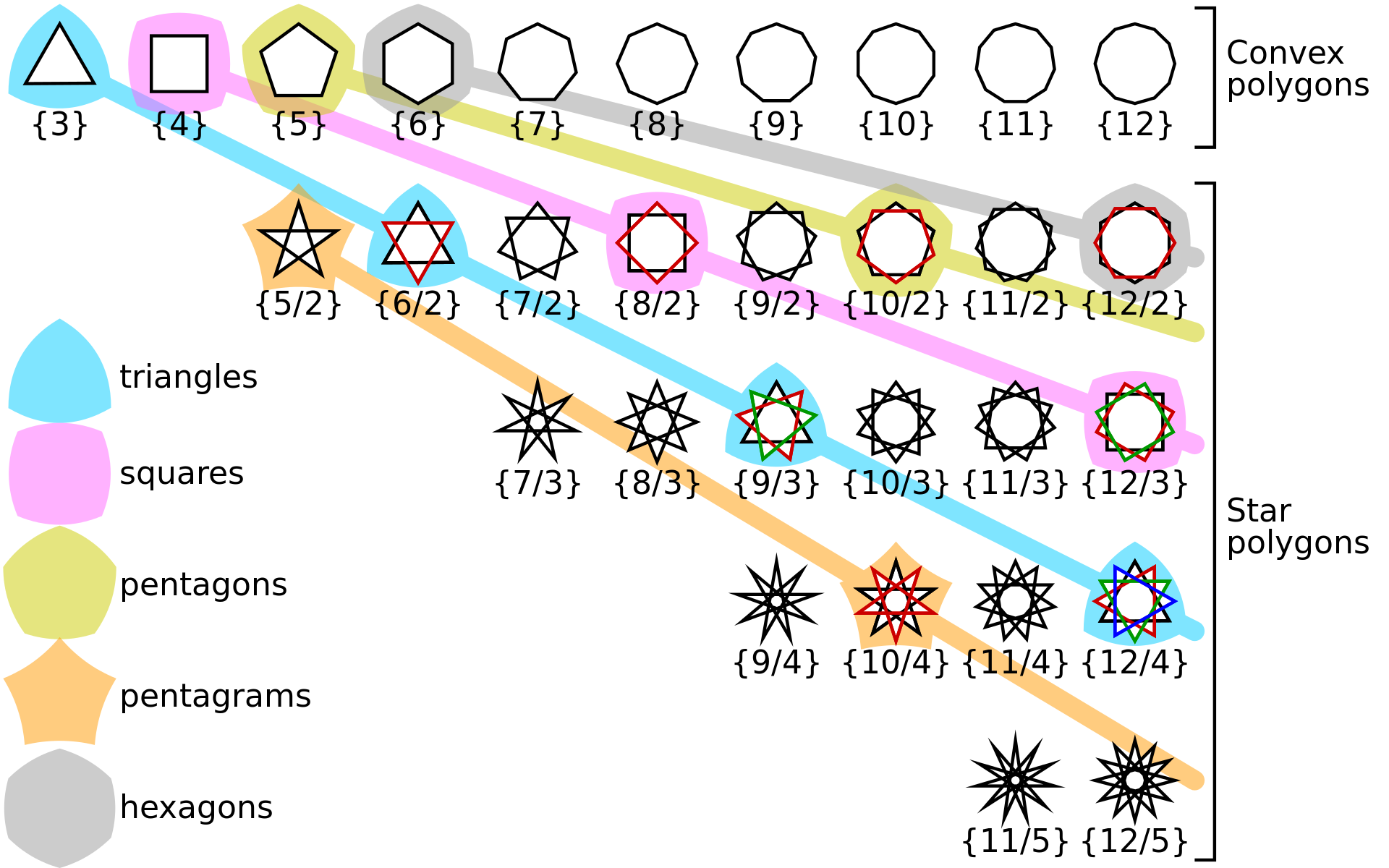
正多面体的施莱夫利符号计做$\{p,q\}$，其中 $p$ 代表每个面的边数，而 $q$ 代表每个顶点连接多少条棱。此外，还有三个平面镶嵌，它们的施莱夫利符号如下：

正四面体：{3,3}
正六面体：{4,3}
正八面体：{3,4}
正十二面体：{5,3}
正二十面体：{3,5}
正三角形镶嵌：{3,6}
正四边形镶嵌：{4,4}
正六边形镶嵌：{6,3}