|
|
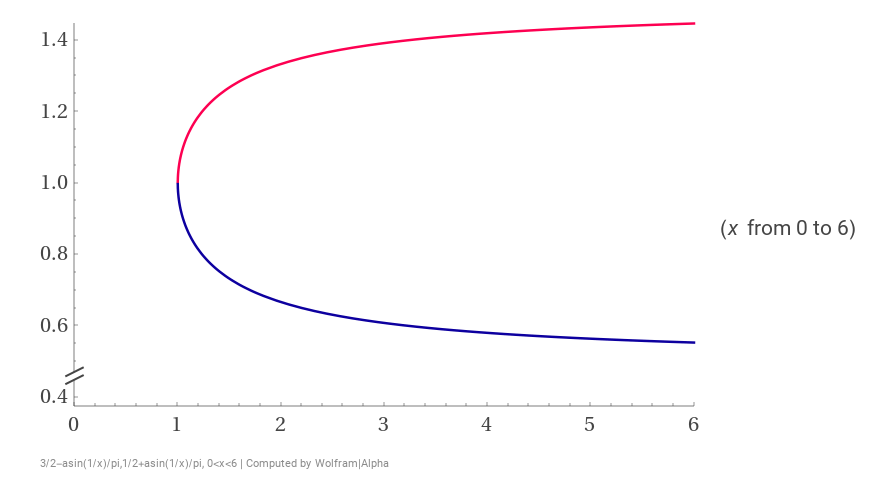
| \begin{array}ly=\frac32-\csc^{-1}(x)/\pi\\y=\frac12+\csc^{-1}(x)/\pi\end{array} |
|
反演:
但是因为$\csc(x),0<x<\pi$是正数,把它乘以常数$k$不会与$x$轴有交点,反演后不会超过半圆
它们覆盖的区域是
问题:怎么做一个类似于
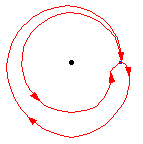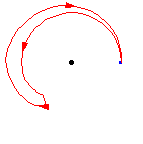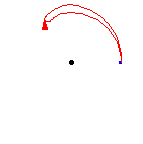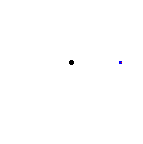 的图?
的图?
$0<r_1<r_2$
圆$C_1(t)=(r_1\cos(t),r_1\sin(t)),t\in[0,1]$
圆$C_2(t)=(r_2\cos(t),r_2\sin(t)),t\in[0,1]$
$f_s(t),t\in[0,1]$是含有连续参数$s\in(0,1)$的连续曲线, $f(0)=f(1)=(0,0)$.
当$s$取遍$(0,1)$时曲线$f_s$覆盖$C_1$与$C_2$之间的区域
当$s\to0$时$f_s(t)$为$C_1(t)$与$C_2(1-t)$的连接.
$$\lim_{s\to0}f_s(t)=\begin{cases}(r_1\cos(2t),r_1\sin(2t))&t\in[0,1/2]\\(r_2\cos(2-2t),r_2\sin(2-2t))&t\in[1/2,1]\end{cases}$$
当$s\to1$时$f_s(t)$为一个点$(0,0)$.
$$\lim_{s\to1}f_s(t)=(0,0),\;t\in[0,1]$$ |
|