中心投影法

hbghlyj

尤承业 书228-229页 题

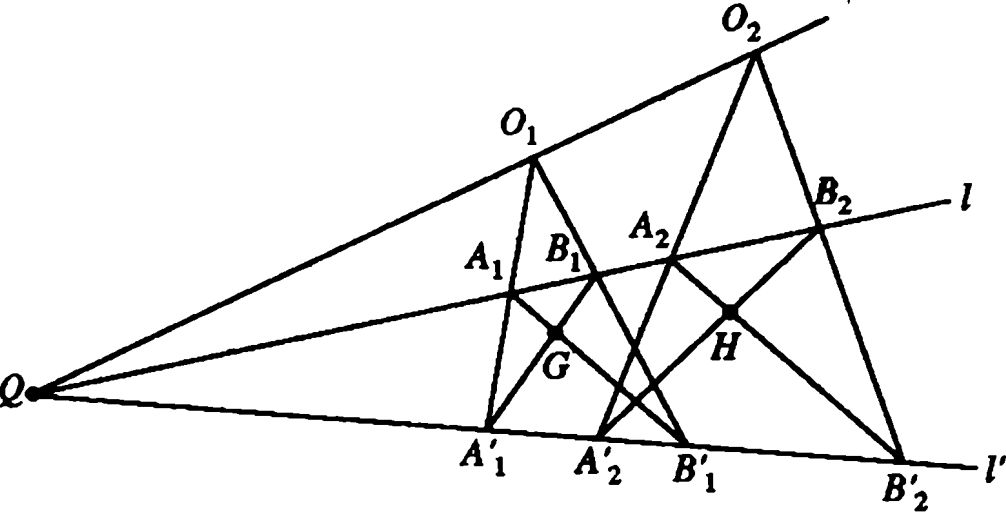
(2) 如果直线 $l$ 和 $l^{\prime}$ 相交于点 $Q$, 点 $O_1, O_2$ 和 $Q$ 共线. 过 $O_1$ 的两条直线分别和 $l$ 相交于 $A_1, B_1$, 和 $l^{\prime}$ 相交于 $A_1^{\prime}, B_1^{\prime}$, 过 $O_2$ 的两条直线分别和 $l$ 相交于 $A_2, B_2$, 和 $l^{\prime}$ 相交于 $A_2^{\prime}, B_2^{\prime}$, 设 $A_1 B_1^{\prime}$ 和 $A_1^{\prime} B_1$ 相交于点 $G$, $A_2 B_2^{\prime}$ 和 $A_2^{\prime} B_2$ 相交于点 $H$, 证明 $Q, G, H$ 共线.

hbghlyj

设$O_1G$交$l,l'$于$C_1,C_1'$,
$O_2H$交$l,l'$于$C_2,C_2'$,
则$(O_1G;C_1C_1')=(O_2H;C_2C_2')=-1$, 以$Q$为中心投影将$O_1,C_1,C_1'$映射到$O_2,C_2,C_2'$, 故$G$映射到$H$.