|
|
Parbelos由三个抛物线弧组成,它们的高度为底部宽度的四分之一(使得焦点位于直线上)。两个较小的抛物线弧相邻放置,它们的底部在同一条直线上,最大的抛物线弧则放置在两个较小抛物线上方,使其宽度等于较小抛物线弧宽度之和。

| 由点B和三个抛物线弧的中点M、M₁、M₂形成的四边形BM₂MM₁是一个平行四边形,其面积与Parbelos的面积相关:\[ F_{\text{平行四边形}}={\frac {3}{4}}F_{\text{Parbelos}} \] |
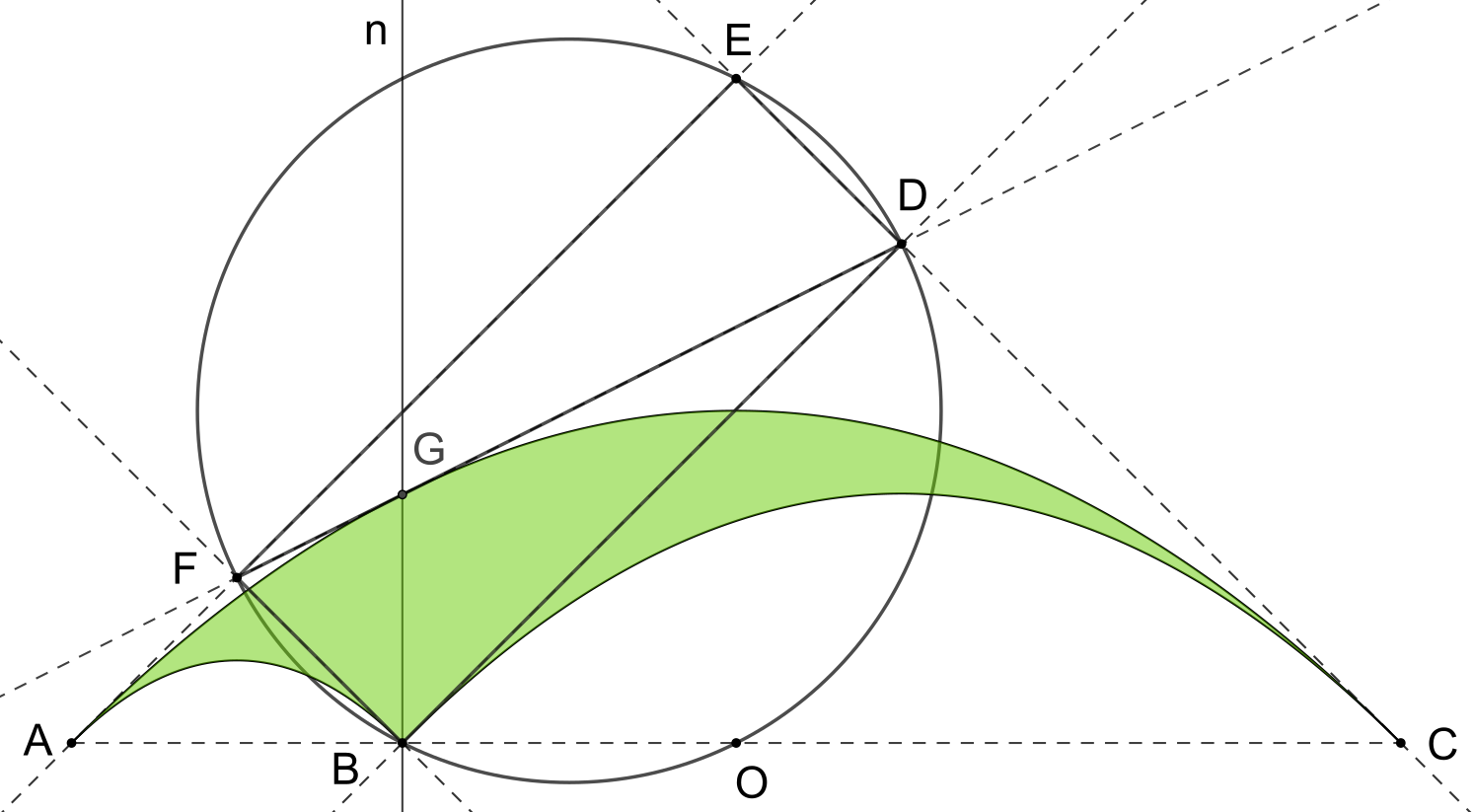
| 三个点$A,B,C$处的四条切线相交于四个点,形成一个矩形$BDEF$,称为切线矩形。切线矩形的外接圆通过$AB$中点$O$,也就是外部抛物线的焦点。切线矩形的对角线之一与外部抛物线相切,切点在点B处的底边垂线上。切线矩形的面积满足:\[ F_{\text{矩形}}={\frac {3}{2}}F_{\text{Parbelos}} \] |
|
|