一道初中几何题求几何方法

hjfmhh

请教大神们，先谢谢了

kuing

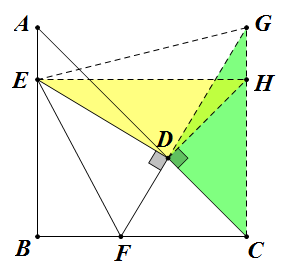
如图，先作等腰 `\Rtt CDH`，由条件知 `BE=CH`，所以 `BCHE` 为矩形。

然后延长 `FD` 和 `CH` 交于 `G`，则由 `\angle EDG=\angle EHG=90\du` 知 `DEGH` 四点共圆，于是有 `\angle DGE=\angle DHE=45\du`，可见 `\triangle DGE` 也是等腰 `\Rtt`，由此易证 `\triangle EDH\cong\triangle GDC`（黄绿全等），所以 `CG=EH=BC`，也就是说 `ABCG` 是正方形。

这样就变成了很常见的初中题：
在正方形 `ABCG` 中，`E`, `F` 在 `AB`, `BC` 上且 `\angle EGF=45\du`，求证 `EF=AE+FC`。
（证明就不写了）