|
|
 kuing
kuing
posted 2024-2-23 14:56
Last edited by kuing 2024-2-23 15:14这个对称作得好😃这样论证起来确实好多了
至于普遍性问题,我猜想多边形都一定是在顶点处取最小。
这只需证明:
对于正三角形内的任意一条线段,都一定是在端点处取最小。
论证可能需要凸性啥的。
(甚至正三角形还可以改为任意给定的三角形)
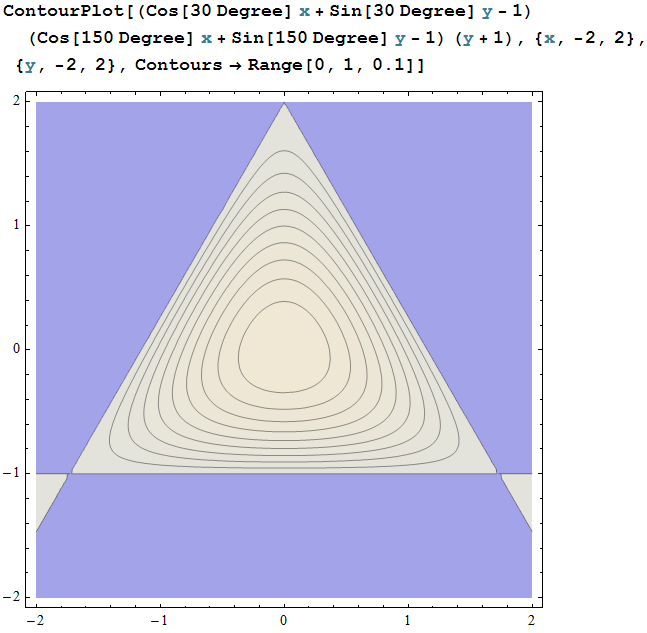
考虑使 $P_1P_2P_3=k$ 的点的轨迹,先用 mma 画来看看:
(正放到坐标系上且中心为原点,不妨设内切圆半径为 1)
- ContourPlot[(Cos[30 Degree] x + Sin[30 Degree] y -
- 1) (Cos[150 Degree] x + Sin[150 Degree] y - 1) (y + 1), {x, -2,
- 2}, {y, -2, 2}, Contours -> Range[0, 1, 0.1]]
|
|