根与系数关系的非对称恒等式

青青子衿

对于三次方程
\[ax^3+bx^2+cx+d=0\]
利用三角函数可以直接推出如下根与系数关系的非对称恒等式
\begin{align*}
\left(x_1+\frac{b}{3 a}\right) \left(x_2+\frac{b}{3 a}\right)=\left(x_3+\frac{b}{3 a}\right)^2+\frac{3 a c-b^2}{3 a^2}
\end{align*}
这样的恒等式有推广吗？有没有该形式的非对称韦达公式？

1. (#1+b/(3a))(#2+b/(3a))-(#3+b/(3a))^2-(3a*c-b^2)/(3a^2)&@@Flatten[Values[Solve[a*x^3+b*x^2+c*x+d==0,x]]]//FullSimplify

Copy the Code

hbghlyj

青青子衿 发表于 2023-1-28 13:10
利用三角函数

可以不用三角函数：

$b=0$时$\frac ca=x_1x_2+(x_1+x_2)x_3=x_1x_2-x_3^2$
\[
x_1x_2=x_3^2+\frac ca
\]

lemondian

任何一个三次方程都可以写成三角函数的形式吗？
如何操作的？

hbghlyj

Wantzel 也是第一个在 1843 年证明，当一个有理系数三次多项式有三个实根但在 $\Bbb Q[x]$ 中不可约时（所谓的 casus impreducibilis)，则根不能只用实数的根式来表示，也就是说，如果用系数的根式来表示根，则必须涉及虚数。

Pierre Wantzel

Wantzel was also the first person who proved, in 1843, that when a cubic polynomial with rational coefficients has three real roots but it is irreducible in $\Bbb Q[x]$ (the so-called casus irreducibilis), then the roots cannot be expressed from the coefficients using real radicals alone, that is, complex non-real numbers must be involved if one expresses the roots from the coefficients using radicals. This theorem would be rediscovered decades later by (and sometimes attributed to) Vincenzo Mollame and Otto Hölder.

hbghlyj

lemondian 发表于 2024-4-25 00:23
任何一个三次方程都可以写成三角函数的形式吗？
如何操作的？

視頻 Solving a Cubic Equation Using a Triangle

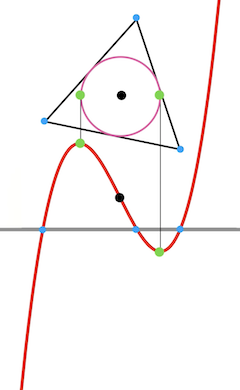
当${q^{2} \over 4}+{p^{3} \over 27}<0$，三个根都是实数，是一个正三角形的頂點的投影
en.wikipedia.org/wiki/Cubic_equation#Trigonom … hyperbolic_solutions
The formula can be proved as follows: Starting from the equation $t^3 + pt + q = 0$, let us set $t = u\cos θ$. The idea is to choose $u$ to make the equation coincide with the identity
    $ 4\cos ^{3}\theta -3\cos \theta -\cos(3\theta )=0. $
For this, choose $ u=2\,{\sqrt {-{\frac {p}{3}}}}\,, $ and divide the equation by $ {\frac {u^{3}}{4}}. $ This gives
    $ 4\cos ^{3}\theta -3\cos \theta -{\frac {3q}{2p}}\,{\sqrt {\frac {-3}{p}}}=0. $
Combining with the above identity, one gets
    $ \cos(3\theta )={\frac {3q}{2p}}{\sqrt {\frac {-3}{p}}}\,, $
and the roots are thus
    $ t_{k}=2\,{\sqrt {-{\frac {p}{3}}}}\,\cos \left[{\frac {1}{3}}\arccos \left({\frac {3q}{2p}}{\sqrt {\frac {-3}{p}}}\right)-{\frac {2\pi k}{3}}\right]\qquad {\text{for }}k=0,1,2. $

kuing

前两天在 forum.php?mod=viewthread&tid=12278#pid59563 里推导的恒等式，算不算是标题说的“根与系数关系的非对称恒等式”？

hbghlyj

$$\left(x_1+\frac{b}{3 a}\right) \left(x_2+\frac{b}{3 a}\right)-\left(x_3+\frac{b}{3 a}\right)^2=\frac13 (-x_1^2 - x_2^2 - x_3^2 + x_1 x_2 + x_1x_3 + x_2 x_3)$$关于三个根对称。