Geodesic Coordinates

hbghlyj

Coordinate systems for the hyperbolic plane: Polar coordinate system

上半平面的坐标$(x,y)$，其中$x\inR,y\inR^+$
$(x,y)$转换为极坐标：$\cases{x=e^v \tanh u\\ y=e^v \operatorname{sech} u}$
反过来，极坐标转换为$(x,y)$：$\cases{u=\sinh^{-1} \frac{x}{y}\\ v=\log\sqrt{x^2+y^2}}$
所以$u,v$的范围是$u,v\inR$

这其实不仅限于“双曲平面”。取2组正交的geodesic用弧长为坐标，见Geodesic Polar Coordinates
page 77
5 Geodesic Coordinates

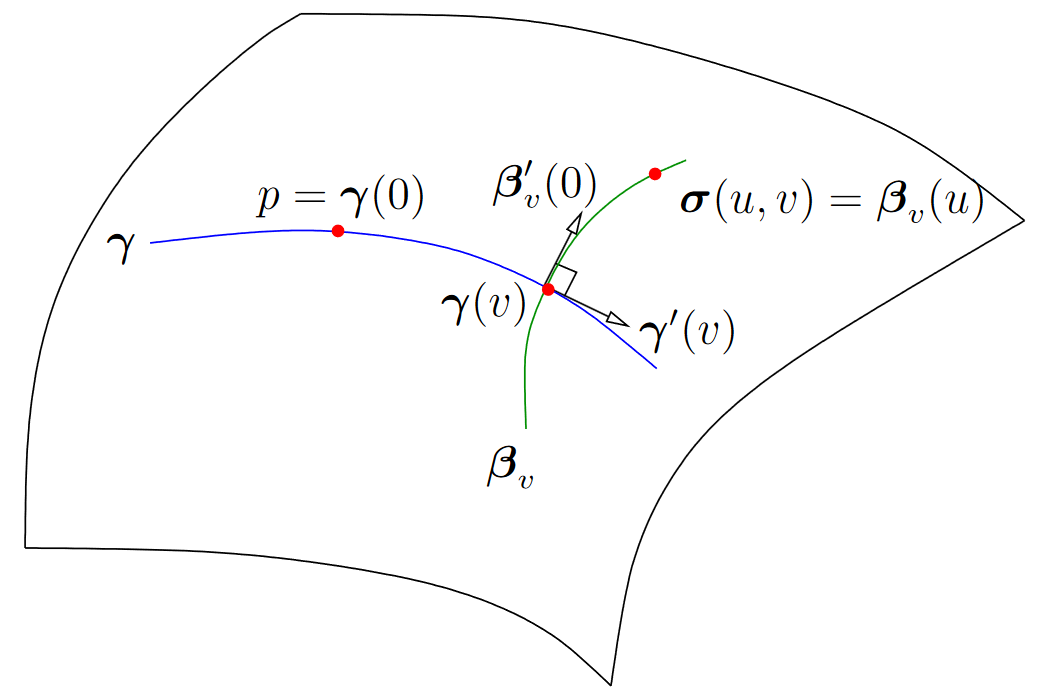
验证：
$d u^2+\cosh ^2 u d v^2$ 作代换 $x=e^v \tanh u, y=e^v \operatorname{sech} u$
得到Poincaré metric $\left(d x^2+d y^2\right) / y^2$.

hbghlyj

hbghlyj 发表于 2024-5-17 15:06
$d u^2+\cosh ^2 u d v^2$ 作代换 $x=e^v \tanh u, y=e^v \operatorname{sech} u$
得到Poincaré metric $\left(d x^2+d y^2\right) / y^2$.

計算有些繁瑣，用WolframAlpha:
Simplify (Dt[ e^v tanh u]^2 + Dt[e^v sech u]^2)/(e^v sech u)^2

hbghlyj

hbghlyj 发表于 2024-5-17 15:09
$d u^2+\cosh ^2 u d v^2$ 作代换 $x=e^v \tanh u, y=e^v \operatorname{sech} u$
得到Poincaré metric $\left(d x^2+d y^2\right) / y^2$.

反过来算，更加繁琐：将$\cases{u=\sinh^{-1} \frac{x}{y}\\ v=\log\sqrt{x^2+y^2}}$代入$d u^2+\cosh ^2 u d v^2$
用WolframAlpha:
Simplify Dt[ArcSinh[x/y]]^2+(1+(x/y)^2)Dt[Log[x^2+y^2]/2]^2


这个要是手算就需要很长时间

hbghlyj

还有一种坐标：horocyclic coordinates
Wikipedia: Horocycle-based coordinate system

the metric tensor is $d\rho^2 + e^{2\rho} dt^2$
https://math.stackexchange.com/q ... urface?noredirect=1