|
|
 kuing
kuing
posted 2024-5-25 23:58
等价于 ABCD 固定在坐标轴上,P 在半径为 2 的圆上动,如下图:
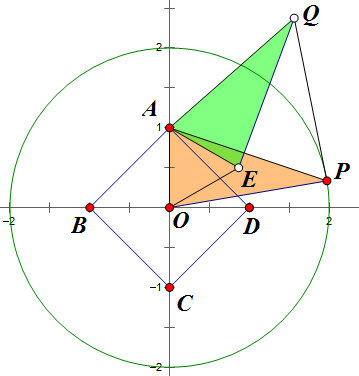
作正△AOE,则易知那两个颜色的三角形全等,所以 QE=2,即 Q 的轨迹为圆,于是 OQ∈[1,3];
第二问(其实反过来动主要是为了这一问,仅第一问并不需要):
设 `P(2\cos t,2\sin t)`,则
\[Q\left(\frac{\sqrt3}2+2\cos(60\du+t),\frac12+2\sin(60\du+t)\right),\]
所以
\begin{align*}
x+y&=\frac{\sqrt3}2+2\cos(60\du+t)-2\cos t+\frac12+2\sin(60\du+t)-2\sin t\\
&=\frac{\sqrt3+1}2-2\sin(30\du+t)+2\cos(30\du+t)\\
&\in\left[\frac{\sqrt3+1}2-2\sqrt2,\frac{\sqrt3+1}2+2\sqrt2\right].
\end{align*} |
|