来自某教师群的简单含参三元不等式

kuing

云浮周(4570****) 10:34:12
各位大神救命啊，被学生问住了

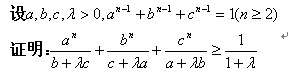
云浮周(4570****) 10:40:07
这个题应该是先用柯西不等式吧，得到的式子非常对称，但找不到办法处理了
汕头 瞬(1017******) 10:40:36
柯西不等式 不是说不考么
云浮周(4570****) 10:41:21
是啊，这学生明显想来拿奥数题来为难老师的
又不能跟他说不要做，烦啊
高三的学生就叫他不用做了，高二的学生还是想鼓励下啊
……
……

原不等式等价于
\[\sum\frac{a^n}{b+\lambda c}\geqslant\frac1{1+\lambda}\sum a^{n-1},\]
由柯西不等式有
\[\sum\frac{a^n}{b+\lambda c}=\sum\frac{(a^{n-1})^2}{a^{n-2}(b+\lambda c)}\geqslant\frac{\left( \sum a^{n-1} \right)^2}{\sum a^{n-2}(b+\lambda c)},\]
于是只要证
\[\frac{\sum a^{n-1}}{\sum a^{n-2}(b+\lambda c)}\geqslant\frac1{1+\lambda},\]
去分母整理为
\[\sum a^{n-1}-\sum a^{n-2}b+\lambda\left( \sum a^{n-1}-\sum a^{n-2}c \right)\geqslant0,\]
显然成立。

其妙

由均值不等式可知，对任何正数$t$，都有$\dfrac{a^n}{b+\lambda c}+t(b+\lambda c)a^{n-2}\geqslant 2\sqrt t a^{n-1}$，

即：$\dfrac{a^n}{b+\lambda c}\geqslant 2\sqrt t a^{n-1}-t(b+\lambda c)a^{n-2}$，对上式求和，并最后取$\sqrt t=\dfrac{1}{1+\lambda}$得，

$\sum\dfrac{a^n}{b+\lambda c}\geqslant 2\sqrt t\sum a^{n-1}-t\sum(b+\lambda c)a^{n-2}\geqslant2\sqrt t\sum a^{n-1}-t(1+\lambda) \sum a^{n-1}=2\sqrt t -(1+\lambda)t=\dfrac1{1+\lambda}$.

这里用了排序不等式$\sum(b+\lambda c)a^{n-2}=\sum ba^{n-2}+\lambda \sum ca^{n-2}\leqslant \sum a^{n-1}+\lambda \sum a^{n-1}=1+\lambda$，$Done$！