周期

reny

定义在$R$上的函数$y=f(x)$,满足$f(x+2)=-\dfrac{1}{f(x)}$,问：$f(x)$有比4更小的正周期吗？
补充：定义在$R$上的函数$y=f(x)$,满足$f(x+2)=-f(x)$,问：$f(x)$也有比4更小的正周期吗？

kuing

设
\begin{align*}
D_1&=\bigcup_{k\in\Bbb Z}\left[\frac43k,\frac43k+\frac23\right),\\
D_2&=\bigcup_{k\in\Bbb Z}\left[\frac43k+\frac23,\frac43k+\frac43\right),
\end{align*}
构造
\[f(x)=\begin{cases}
1, & x\in D_1,\\
-1,& x\in D_2,
\end{cases}\]
它满足条件，并且最小正周期为 $4/3$。

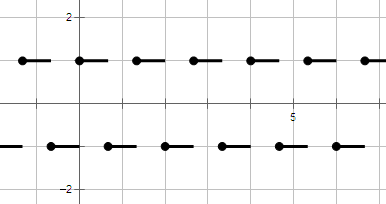
图象：

reny

回复 2# kuing
厉害！感谢kk!

isee

这个，我每次都说4是周期，是不是最小，从来只是一闪而过。

设
\begin{align*}
D_1&=\bigcup_{k\in\Bbb Z}\left[\frac43k,\frac43k+\frac23\right),\\
D_2&=\bigcup_{k ...
kuing 发表于 2013-12-6 15:11

一如继往的强


这个构造，也许从侧面说明，要使其为最小正整数周期，怕得附加严格的条件，并不容易。