证明轨迹与圆正交

hbghlyj

设 $D,E,F$ 是圆 $\cal C$ 上的三个点。
四次曲线 $\cal Q$ 是 $PD\pm PE\pm PF=0$ 的 $P$ 轨迹。如何证明 $\mathcal C$ 与 $\mathcal Q$ 在 4 个点处正交？

kuing

这个轨迹是如何在 GGB 里画出来的？可以说一下作法步骤嘛？

==========

哦有办法了，先任作三点 A、B、C，然后直接输入

1. sqrt((x-x(A))^2+(y-y(A))^2)-sqrt((x-x(B))^2+(y-y(B))^2)-sqrt((x-x(C))^2+(y-y(C))^2)=0

Copy the Code

回车即可。
再作另外两条

1. sqrt((x-x(A))^2+(y-y(A))^2)+sqrt((x-x(B))^2+(y-y(B))^2)-sqrt((x-x(C))^2+(y-y(C))^2)=0

Copy the Code

和

1. sqrt((x-x(A))^2+(y-y(A))^2)-sqrt((x-x(B))^2+(y-y(B))^2)+sqrt((x-x(C))^2+(y-y(C))^2)=0

Copy the Code

至于哪条方程有轨迹得视 A、B、C 的位置而论，似乎一般都是两条有另一条没有。

==========

要么，利用 `(a + b + c) (a - b - c) (a - b + c) (a + b - c) = \sum a^4-2\sum b^2c^2`，应该可以一次过作出来，而不用作三次……

kuing

用速度分解很容易证，以 `PA-PB-PC=0` 为例：

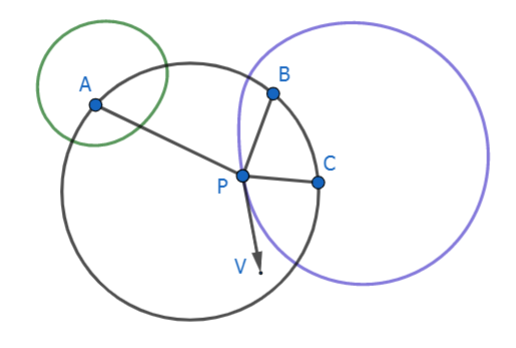
如上图，设 `P` 为 `PA-PB-PC=0` 的轨迹上的动点，其速度为 `\bm v`，则它在 `AP` 上的速度分量大小为 `v\cos\bigl\langle\bm v,\vv{AP}\bigr\rangle`，另外两者同理，既然轨迹使 `PA-PB-PC` 为常数，则三个速度分量必然满足 `v\cos\bigl\langle\bm v,\vv{AP}\bigr\rangle-v\cos\bigl\langle\bm v,\vv{BP}\bigr\rangle-v\cos\bigl\langle\bm v,\vv{CP}\bigr\rangle=0`。

于是，要证明轨迹与圆正交，只需证如下几何题：

如下图，圆 `O` 上有四点 `A`, `B`, `C`, `P` 满足 `PA-PB-PC=0`，求证：`\cos\angle APO-\cos\angle BPO-\cos\angle CPO=0`。

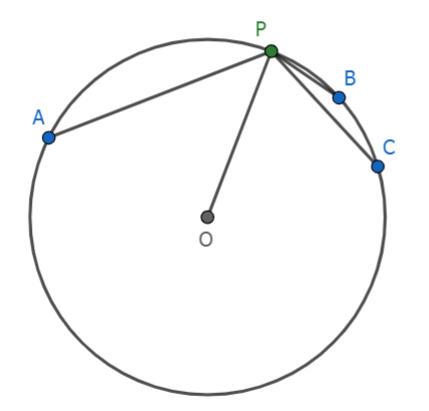
证明：设圆半径为 `R`，则显然有 `PA=2R\cos\angle APO` 等，代入即得证。

hbghlyj

kuing 发表于 2024-12-22 07:30
用速度分解很容易证，以 `PA-PB-PC=0` 为例：

如上图，设 `P` 为 `PA-PB-PC=0` 的轨迹上的动点，其速度为  ...

一个类似的问题：求证阿氏圆与外接圆正交。

$PB:PC=AB:AC$ 的 $P$ 轨迹与 $ABC$ 的外接圆在 2 个点处正交？

用速度分解，设 `P` 为 $PB:PC=AB:AC$ 的轨迹上的动点，其速度为 `\bm v`，则 $v\cos\bigl\langle\bm v,\vv{BP}\bigr\rangle:v\cos\bigl\langle\bm v,\vv{CP}\bigr\rangle=AB:AC$

所以 $\bm v$ 通过 $ABC$ 的外心 $O$

hbghlyj

kuing 发表于 2024-12-22 07:30
用速度分解很容易证，以 `PA-PB-PC=0` 为例：

如上图，设 `P` 为 `PA-PB-PC=0` 的轨迹上的动点，其速度为  ...

有一个类似的问题，可以用速度分解的方法解决吗？
kuing.cjhb.site/forum.php?mod=viewthread&tid=7973

“AP和BP分别等于E的横纵坐标” 相当于说它们满足某条直线的方程。