|
|
源自知乎提问区
求 $f(x)=\sin x(1+\cos x)$ 求最大值
简单分析 $f(x)=\sin x(1+\cos x)$ 求最大值,只需考察 $x\in(0,\pi)$ 的情形.
而 $x\in[\pi/2,\pi)$ 时,令 $\xi+x=\pi$ , $\xi\in(0,\pi/2]$ ,则 \[\sin x(1+\cos x)=\sin\xi(1-\cos\xi)\leqslant\sin \xi(1+\cos\xi),\] 即 $f(x)$ 的最大值归结为 $x$ 为非钝角的情形,考察内接于单位圆 D 的等腰三角形 ABC(逆时针顺序),其中 AC=BC.
图 1
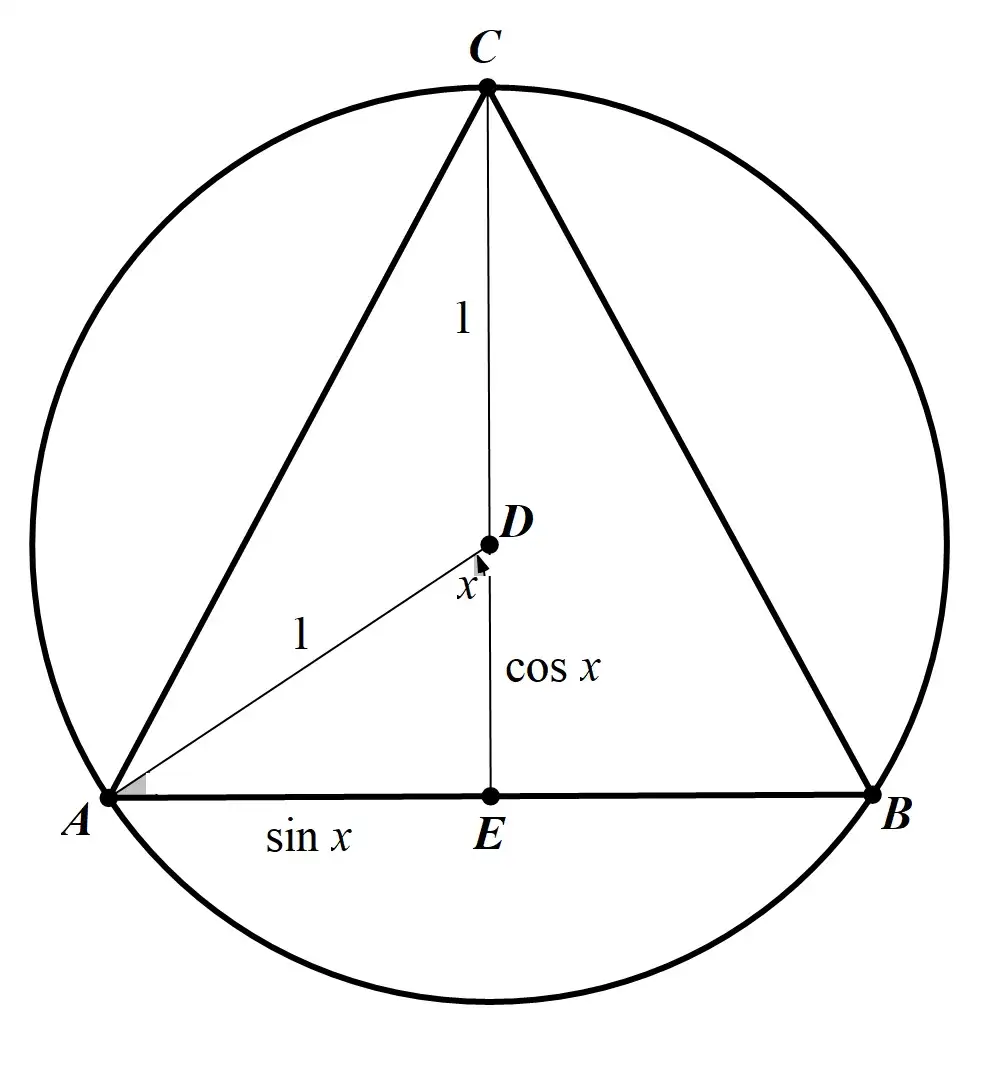
连接 DA,并设 $\angle ADE=x$ ,则 $AE=\sin x$ ,AB 边上的高 $h_c=CE=1+\cos x$ ,如图 1 所示,其中 E 为 AB 中点.
于是 \[\sin x(1+\cos x)=AE\cdot CE=S_{\triangle ABC},\] 而内接于圆的三角形为正三角形时面积最大,且最大值为 $\frac{3\sqrt3}4=f(\pi/3)>1=f(\pi/2)$ .
|
|