|
|
 kuing
kuing
posted 2024-12-30 15:18
Last edited by kuing 2024-12-30 15:28
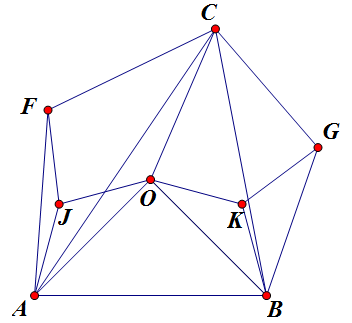
如上图,设 `O` 为 `\triangle ABC` 外心,以 `OA`, `OB` 为底边向外作顶角为 `120\du` 的等腰 `\triangle OJA` 和 `\triangle OKB`。
易证 `\triangle AJF\sim\triangle AOC` 且 `\triangle BKG\sim\triangle BOC`,相似比 `1:\sqrt3`,故 `JF=KG=OC/\sqrt3=2\sqrt{2/3}`。
再计算一下角度,有 `\angle OJF+\angle OKG=240\du-\angle AJF+240\du-\angle BKG=480\du-\angle AOC-\angle BOC=480\du-270\du=210\du`,易知 `\angle OJK=\angle OKJ=15\du`,所以 `\angle FJK+\angle GKJ=240\du`,且不难算出 `JK=2+2/\sqrt3`,于是问题就简化成:
如下图,`JK=2+2/\sqrt3`, `JF=KG=2\sqrt{2/3}`, `\angle FJK+\angle GKJ=240\du`,求 `FG` 的最小值。
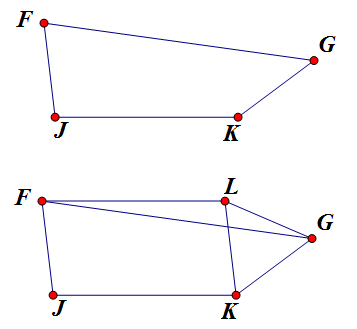
如上图,作平行四边形 `FJKL`,则易知 `\angle LKG=60\du`,所以 `\triangle LKG` 是等边三角形,因此 `FG\leqslant FL+LG=2+2/\sqrt3+2\sqrt{2/3}`,当 `FG\px JK` 时取等。 |
Rate
-
View Rating Log
|