如何证明这个2024年全国2卷圆锥曲线题的拓展？

lemondian

（1）已知有心曲线$C:Ax^2+By^2=1$，点$P_1$在$C$上，$k_1,k_2$为常数，且$k_1 \ne k_2$。按照如下方式依次构造点$P_n(n=2,3,\cdots )$，过$P_{n-1}$作斜率为$k_1$的直线与$C$交于点$Q_{n-1}$，再过$Q_{n-1}$作斜率为$k_2$的直线与$C$交于点$P_n$。设$S_n$为$\triangle P_nP_{n+1}P_{n+2}$的面积，证明：对任意的正整数$n$，$S_n=\dfrac{4|AB(A+Bk_1k_2)(k_1-k_2)^3|}{(A+Bk_1^2)^2(A+Bk_2^2)^2}$。



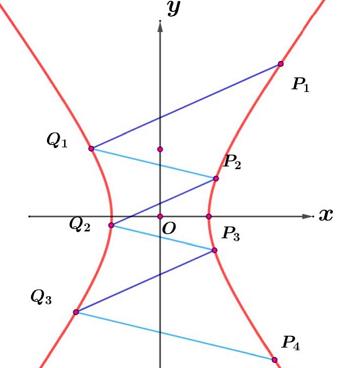
（2）已知抛物线$C:y^2=2px(p>0)$，点$P_1$在$C$上，$k_1,k_2$为常数，且$k_1 \ne k_2$。按照如下方式依次构造点$P_n(n=2,3,\cdots )$，过$P_{n-1}$作斜率为$k_1$的直线与$C$交于点$Q_{n-1}$，再过$Q_{n-1}$作斜率为$k_2$的直线与$C$交于点$P_n$。设$S_n$为$\triangle P_nP_{n+1}P_{n+2}$的面积，证明：对任意的正整数$n$，$S_n=4p^2|\dfrac{1}{k_1}-\dfrac{1}{k_2}|^3$。

kuing

前段时间有微信网友问过我（1）（还有一个 Axn±Byn 等比的结论），我证出来了。
可是我不能发上来，因为我收了他的红包，如果就这样贴上来，对他不公平。

所以我只能给一些提示：
椭圆用三角代换；双曲线用双曲代换（注意双曲函数也有和差化积公式）。
则两点连线斜率可表为一个简单的表达式，然后会得出一个等差的结论。
计算面积时使用 2S = |x1y2 − y1x2 + x2y3 − y2x3 + x3y1 − y3x1| 这个公式，然后需要一些双曲变换/三角变换。

kuing

点评
snowblink    见《数学通讯》12月下半文章：《圆锥曲线上的“漂亮点列”及其性质——由2024年新高考2卷第19题引发的探究》

多谢 @snowblink
我搜到电子版了😁：
mp.weixin.qq.com/s?__biz=MzU2MTI2NTE0Mg==& … 30cf12d&scene=27
看来不用代换直接证也不难……

力工

kuing 发表于 2025-1-12 23:15
前段时间有微信网友问过我（1）（还有一个 Axn±Byn 等比的结论），我证出来了。
可是我不能发上来，因为我 ...

应该是发了文章了的。