阿达玛不适定例子

hbghlyj

適定性問題來自於數學家 Hadamard 所給出的定義。他認為物理現象中的數學模型應該具備下述性質：

• 存在解
• 解是唯一的
• 解隨著起始條件連續的改變

1. DSolve[Laplacian[u[x, y], {x, y}] == x^2 + 3 x y + y^2, u[x, y], {x, y}]

Copy the Code

$u(x,y)= c_1(x-i y)+ c_2(x+i y)+\frac{1}{2} \left(x^3 y+x^2 y^2\right)$
特解
$$u_1(x,y):=\frac{1}{12} \left(x^4+6 x^3 y+y^4\right)$$

1. Clear[u1]
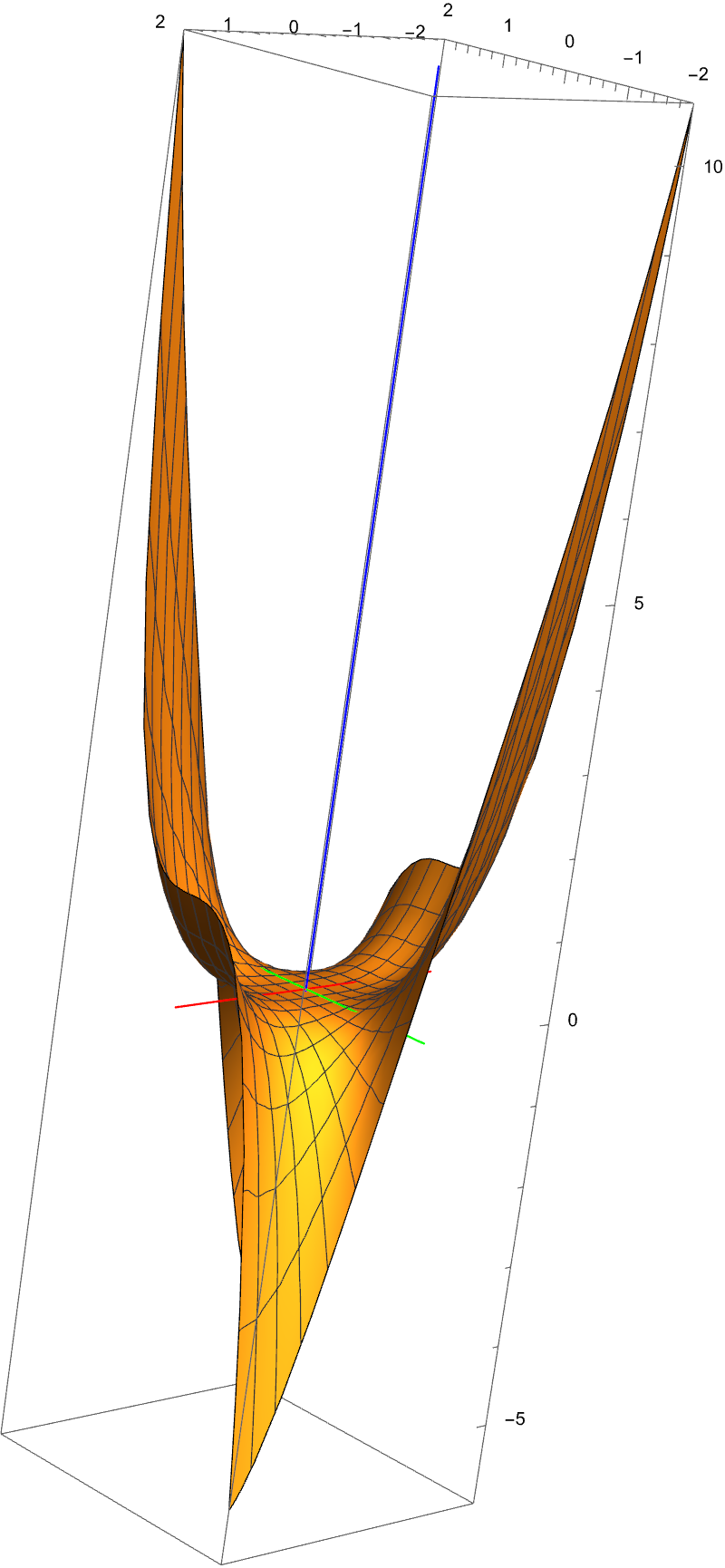
2. u1[x_,y_]:=(x^4+6 x^3  y +y^4)/12;
4. Xaxe=ParametricPlot3D[{x,0,0},{x,-2,2},PlotRange->{{-2, 2},{-2,2},{-6,10.7}},ImageSize->400, PlotStyle -> {Thickness[0.003],Green}];
5. Yaxe=ParametricPlot3D[{0,y,0},{y,-2,2},PlotRange->{{-2, 2},{-2,2},{-6,10.7}},ImageSize->400, PlotStyle ->{ Thickness[0.003],Red}];
6. Zaxe=ParametricPlot3D[{0,0,z},{z,-6,10.7},PlotRange->{{-2, 2},{-2,2},{-6,10.7}},ImageSize->400, PlotStyle ->{ Thickness[0.003],Blue}];
7. u1graph=Plot3D[u1[x,y],{x,-2,2},{y,-2,2},PlotRange->{{-2, 2},{-2,2},{-6,10.7}},ImageSize->400, PlotStyle -> Thickness[0.003]];
8. Show[Xaxe,Yaxe,Zaxe,u1graph]

Copy the Code

hbghlyj

逆問題通常是不適定的。见 elliptic PDE 的例子：
$u_1(x,y)=0$
$u_2(x,y)=\dfrac{\sin (n x) \sinh (n y)}{n^{k+1}}$
则有

$\displaystyle\left| {{u_1}\left( 0,y \right) - {u_2}\left(0,y\right)} \right|$ 当 $n\to\infty$ 时趋于 0 udivy[n_, x_] := 1/n^k Sin[n x]; frames = Table[     Plot[udivy[n, x], {x, 0, Pi}, PlotRange -> {{0, Pi}, {-1, 1}},      ImageSize -> 600], {n, 1, 20}]; Export["output.gif", frames, "DisplayDurations" -> 0.1] Copy the Code

$\displaystyle\left| {{u_1}\left( {\frac{\pi }{2},y} \right) - {u_2}\left( {\frac{\pi }{2},y} \right)} \right| = \frac{\sinh (ny)}{n^2} = \frac{{{e^{ny}} - {e^{ - ny}}}}{{2{n^2}}}$ 当 $n\to\infty$ 时趋于无穷 Clear[u] k=1; u[n_,x_,y_]:=1/n^(k+1) Sin[n x] Sinh[n y]; frames=Table[Plot3D[u[n,x,y],{x,0,Pi},{y,0,3},PlotStyle->Thickness[0.003]],{n,1,10,1}]; Export["animation.gif",frames,"DisplayDurations"->0.25] Copy the Code