单位球体积最小的外切八面体

hejoseph

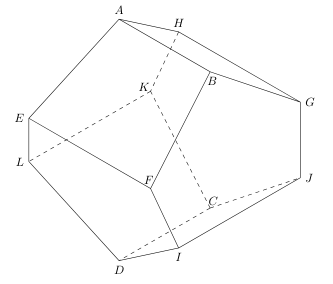
单位球体积最小的外切八面体是如下图的多面体，它由 $4$ 个四边形面和 $4$ 个五边形面构成顶点的坐标分别是 $A$：$(0,-b,h_2)$，$B$：$(0,b,h_2)$，$C$：$(-b,0,-h_2)$，$D$：$(b,0,-h_2)$，$E$：$(c,-a,h_1)$，$F$：$(c,a,h_1)$，$G$：$(-c,a,h_1)$，$H$：$(-c,-a,h_1)$，$I$：$(a,c,-h_1)$，$J$：$(-a,c,-h_1)$，$K$：$(-a,-c,-h_1)$，$L$：$(a,-c,-h_1)$，求出 $a$、$b$、$c$、$h_1$、$h_2$ 的值和这个多面体的体积。

hejoseph

四边形是梯形，两底之间的高为 $\sqrt{c^2+(h_2-h_1)^2}$，面积为 $(a+b)\sqrt{c^2+(h_2-h_1)^2}$。
五边形可分割成一个梯形和一个三角形，梯形两底之间的高为 $\sqrt{(c-a)^2+(2h_1)^2}$，面积为$(a+c)\sqrt{(c-a)^2+(2h_1)^2}$；以梯形其中一底边为底的三角形的高为 $\sqrt{(a-b)^2+(h_2-h_1)^2}$，面积为 $c\sqrt{(a-b)^2+(h_2-h_1)^2}$。
以原点为顶点，各面为底分割成八个棱锥，棱锥的高都是单位球的半径，即 $1$，这些棱锥体积的和就是这个多面体的体积，体积为
\[
\frac{4}{3}\left((a+b)\sqrt{c^2+(h_2-h_1)^2}+(a+c)\sqrt{(c-a)^2+(2h_1)^2}+c\sqrt{(a-b)^2+(h_2-h_1)^2}\right)
\]
与单位球相切得到如下关系
\begin{align*}
h_2^2&=1+\left(\frac{h_2-h_1}{c}\right)^2\\
\left(\frac{a+c}{2}\right)^2&=1+\left(\frac{c-a}{2h_1}\right)^2
\end{align*}
五边形各顶点共面，得到如下关系
\[
\frac{a-b}{h_2-h_1}=\frac{c-a}{2h_1}
\]
问题就变为满足上面三个关系条件下的体积表达式最小值。

根据上面的计算，Mathematica里运行如下命令

1. NMinimize[{4/3((a+b)Sqrt[c^2+(h2-h1)^2]+c Sqrt[(a-b)^2+(h2-h1)^2]+(a+c)Sqrt[(c-a)^2+(2h1)^2]),h2^2==1+((h2-h1)/c)^2&&((a+c)/2)^2==1+((c-a)/(2h1))^2&&(a-b)/(h2-h1)==(c-a)/(2h1)&&0<b<a<c&&0<h1<h2},{a,b,c,h1,h2}]

Copy the Code

得到的结果为
{6.70092, {a -> 0.92933, b -> 0.695926, c -> 1.14368, h1 -> 0.39307,   h2 -> 1.24908}}
但是改为Minimize运行一天都没结果。

hejoseph

下图上面是单位球面上4点到8点构成体积最大的多面体，下面是单位球体积最小的外切4到8面体，上下两个多面体构成了对偶多面体。