|
|
 战巡
战巡
posted 2025-5-20 11:38
之前研究过这个问题
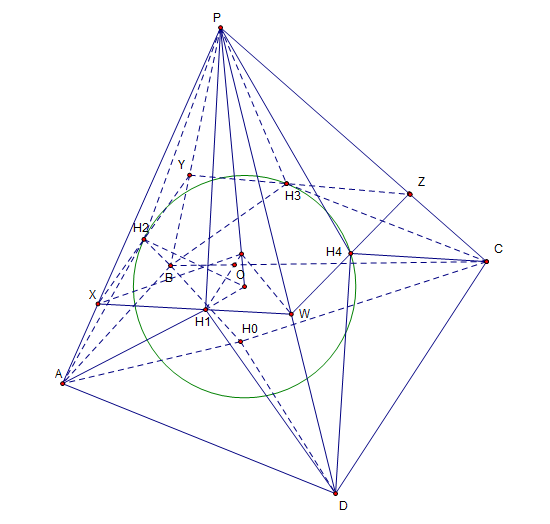
如图,四棱锥$P-ABCD$,有内切球$O$,$H_1,H_2,H_3,H_4,H_0$分别为各面切点。
定理:四棱锥$P-ABCD$存在内切球的充要条件,为$\angle APD+\angle BPC=\angle APB+\angle CPD$。
证明:
必要性:
当内切球存在时,会有$PH_1=PH_2=PH_3=PH_4$,以及$AH_1=AH_2=AH_0, BH_2=BH_3=BH_0, CH_3=CH_4=CH_0, DH_4=DH_1=DH_0$,因此可证明
\[\Delta PAH_1\cong \Delta PAH_2, \Delta PBH_2\cong \Delta PBH_3,\Delta PCH_3\cong\Delta PCH_4,\Delta PDH_4\cong \Delta PDH_1\]
故此
\[\angle APH_1=\angle APH_2,\angle BPH_2=\angle BPH_3,\angle CPH_3=\angle CPH_4,\angle DPH_4=\angle DPH_1\]
然后
\[\angle APD+\angle BPC=\angle APH_1+\angle DPH_1+\angle BPH_3+\angle CPH_3\]
\[=\angle APH_2+\angle DPH_4+\angle BPH_2+\angle CPH_4=\angle APB+\angle CPD\]
充分性:
这个相对麻烦,此时我们可以不管底面,因为如果给定了$PA,PB,PC,PD$四条向量以后,这么个椎体(无底面)有内切球,那么不管底面是什么角度,总会有内切球的。
此时需要重新绘图,上面的切点不再作数(毕竟此时还没证明存在内切球,哪来的什么切点)。
我们还要先定义一种东西:二面角的平分面。
\textbf{定义}:如果一个过两平面交线的平面将这两平面所形成二面角分为两个相等的二面角,称其为此二面角的平分面。
很显然,平分面上任意一点,到二面角所在两平面的距离都相等。
好,下面开始操作。
首先作$B-PA-D$的平分面,以及$A-PD-C$的平分面,它们会交于一条直线,令为$PH$。
在$PA$上任取一点$X$,作$XO'\perp PA$,且$O'$要在$B-PA-D$平分面内,交$PH$于$O'$。
过$O'$作$O'W\perp PD$于$W$,连$XW$,并作$PH_1\perp XW$于$H_1$。
在平面$PAB$和$PCD$内,分别作$\Delta PXH_2\cong\Delta PXH_1$,以及$\Delta PWH_4\cong\Delta PWH_1$,并分别延长$XH_2,WH_4$,与$PB,PC$分别交于$Y,Z$两点。
连$YZ$,并作$PH_3\perp YZ$于$H_3$。
由于上面作的全等,我们知道$\angle XPH_1=\angle XPH_2,\angle WPH_1=\angle WPH_4$,如果加上已知的$\angle APD+\angle BPC=\angle APB+\angle CPD$,会得到
\[\angle YPH_2+\angle ZPH_4=\angle YPZ\]
同时还有$PH_2=PH_1=PH_4$,以及
\[PY\cos(\angle YPH_2)=PH_2=PH_4=PZ\cos(\angle ZPH_4)\]
由于$PH_3\perp YZ$,也会有
\[PY\cos(\angle YPH_3)=PH_3=PZ\cos(\angle ZPH_3)\]
不妨令$\angle YPZ=\theta, \angle ZPH_3=x$,如此有
\[\frac{\cos(\theta-x)}{\cos(x)}=\frac{PZ}{PY}=\frac{\cos(\angle YPH_2)}{\cos(\angle ZPH_4)}=\frac{\cos(\theta-\angle ZPH_4)}{\cos(\angle ZPH_4)}\]
如果令
\[f(x)=\frac{\cos(\theta-x)}{\cos(x)}\]
那么
\[f'(x)=\frac{\sin(\theta)}{\cos^2(x)}>0\]
这说明$f(x)$恒增,其相关方程只能有一个解,故此必须得有
\[x=\angle ZPH_3=\angle ZPH_4\]
以及
\[\angle YPH_2=\angle YPH_3\]
然后
\[\Delta YPH_2\cong\Delta YPH_3,\Delta ZPH_3\cong\Delta ZPH_4\]
即
\[PH_3=PH_2=PH_4=PH_1\]
同时,也会证明出$XH_1=XH_2,YH_2=YH_3,ZH_3=ZH_4,WH_4=WH_1$,即四边形$XYZW$存在内切圆,切点即为$H_1,H_2,H_3,H_4$,令此时$H_1,H_2,H_3,H_4$所在圆的圆心为$O_1$,加上$PH_1=PH_2=PH_3=PH_4$,说明$P$和这个圆构成一个圆锥,且底面圆心即为$O_1$,$PO_1\perp$面$H_1H_2H_3H_4$。
接下来,如果分别过$H_1,H_2,H_3,H_4$作$PH_1,PH_2,PH_3,PH_4$的垂线,与$PO_1$所在直线的交点,很容易证明是重合的,令为$O$,那这个$O$就是内切球的球心。
如此便证明了,在不考虑底面的情况下,四个侧面组成的椎体存在内切球。
对于底面,不管底面在哪,总可以滑动(同时放缩)四侧面的内切球,使其恰好与底面相切。
|
|