焦点弦的垂弦引出的相似

1+1=？

如图，过焦点弦端点的两条垂线与椭圆交于$E,H$二点，作$FG$垂直$EH$，则$FG$平分$∠DGC$.

1+1=？

如图，连接$DH$，$EC$的交点$G$，$DC,EH$的交点P，设$DE$，$CH$的交点$V$(无穷远点)，由完全四点形调和可知$PG$是$V$的极线，可知$PG$过锥线中心，$PG$交$CH$于$M$，由完全四点形可知$V,M$调和分割$C,H$，$M$是$CH$的中点，$PG$是$CH$的共轭径线。
由$DC$垂直$CH$可知它们与无穷远直线的交点是一对对合对应点，由$PG$和$CH$共轭可知它们与无穷远直线的交点也是对合对应点，所以$DC$和$PG$与无穷远直线的交点是射影对应的，又$DC$过焦点，$PG$过原点 ，所以$DC和PG$射影对应，当$DC和Y$轴平行时易知$DC平形PG$它们与无穷远直线的交点重合。
有一对射影对应的点重合时该射影对应为透视对应，所以$DC和PG$透视对应，他们的交点$P$过定直线。

1+1=？

作$FK$垂直$EH$，可知$FKED$四点共圆，$FKHC$四点共圆，可知$∠DKF=∠FKC$

kuing

设 `C`, `D` 在直线 `EH` 上的投影为 `M`, `N`，如上图，有
\[
FG~\text{平分}~\angle DGC
\iff\frac{CM}{DN}=\frac{GM}{GN}\iff\frac{CE}{DH}=\frac{FC}{FD}\iff\angle CFE=\angle DFH,
\]
然后延长 `EC`, `HD` 交准线于 `P`, `Q`，点 `C`, `D` 在准线上的投影为 `C'`, `D'`，如下图：

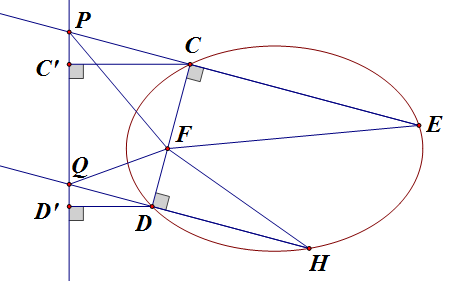
熟知 `FP` 是 `\angle CFE` 的外角平分线，`FQ` 是 `\angle DFH` 的外角平分线，因此
\[\angle CFE=\angle DFH\iff\angle CFP=\angle DFQ\iff\frac{FC}{CP}=\frac{FD}{DQ}\iff\frac{eCC'}{CP}=\frac{eDD'}{DQ},\]
最后一式显然成立，即得证。

（好多比例绕来绕去的，不知有没有绕了弯路……

kuing

从楼上抽出个小结论：



如上图，设 `\angle CFE=2\alpha`，`CE` 与准线的夹角为 `\beta`，则有
\[\tan\alpha=\cot\angle CFP=\frac{FC}{CP}=\frac{eCC'}{CP}=e\cdot\sin\beta.\]