|
|
original poster
1+1=?
posted 2025-6-1 18:03
from mobile
Last edited by 1+1=? 2025-6-2 01:08
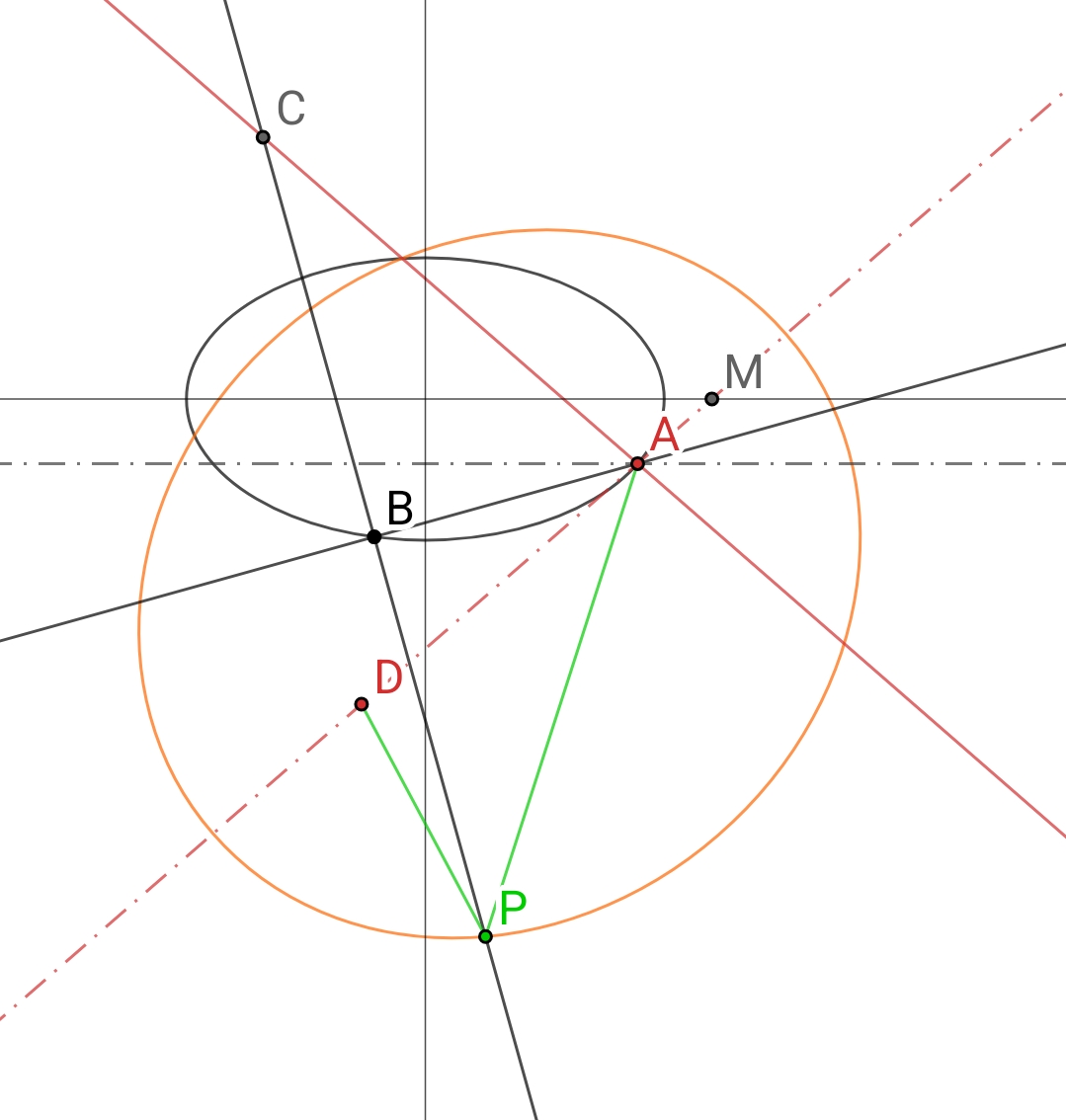 如图,离心率为$e$的椭圆上有$A,B$两点,$A$点关于椭圆的法线为红色直线,它与过点$B$且垂直$AB$的直线交于$C$点,$C$点关于点$B$的对称点为$P$点,法线关于过$A$点水平线的轴对称直线为红色虚线,它与$X$轴交于$M$点,记$λ=\frac{3-e^2}{e^2-1}$,点$D=λA+(1-λ)M$,当点$B$在椭圆上运动时,试证明$PA+PD$为定值且当取不同A点时$P$点轨迹为离心率不变的椭圆.
如图,离心率为$e$的椭圆上有$A,B$两点,$A$点关于椭圆的法线为红色直线,它与过点$B$且垂直$AB$的直线交于$C$点,$C$点关于点$B$的对称点为$P$点,法线关于过$A$点水平线的轴对称直线为红色虚线,它与$X$轴交于$M$点,记$λ=\frac{3-e^2}{e^2-1}$,点$D=λA+(1-λ)M$,当点$B$在椭圆上运动时,试证明$PA+PD$为定值且当取不同A点时$P$点轨迹为离心率不变的椭圆. |
|