|
|
 kuing
kuing
posted 2025-6-15 00:06
Last edited by kuing 2025-6-15 00:42勉强搞出几何证法,但有个地方不够严谨。
先证明如下命题:
命题 1:如下图,`\Rtt OAC` 和 `\Rtt OBD` 的斜边 `AC` 和 `BD` 均与 `\odot O` 相切,`BA` 的延长线与 `CD` 的延长线交于 `P`,记 `\angle OAC=\alpha`, `\angle OBD=\beta`, `\angle AOB=\gamma`, `\angle POA=\theta`,则有 `2\theta=\alpha+\beta-\gamma`。
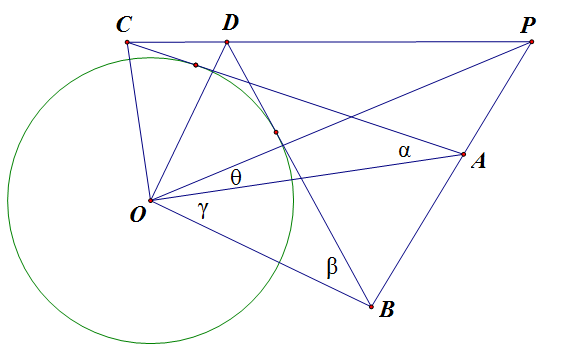
证明:不失一般性,设 `\odot O` 的半径为 `1`,则
\[OA=\frac1{\sin\alpha},~OB=\frac1{\sin\beta},~OC=\frac1{\cos\alpha},~OD=\frac1{\cos\beta},\]
在 `\triangle POB` 中,由张角定理有
\[\frac{\sin(\gamma+\theta)}{OA}=\frac{\sin\gamma}{OP}+\frac{\sin\theta}{OB},\]
在 `\triangle POC` 中,易知 `\angle COD=\gamma`,又由张角定理有
\[\frac{\sin(90\du-\theta)}{OD}=\frac{\sin\gamma}{OP}+\frac{\sin(90\du-\gamma-\theta)}{OC},\]
两式相减化简整理得
\begin{gather*}
\frac{\sin(\gamma+\theta)}{OA}+\frac{\cos(\gamma+\theta)}{OC}=\frac{\sin\theta}{OB}+\frac{\cos\theta}{OD},\\[1ex]
\sin(\gamma+\theta)\sin\alpha+\cos(\gamma+\theta)\cos\alpha=\sin\theta\sin\beta+\cos\theta\cos\beta,\\[1ex]
\cos(\gamma+\theta-\alpha)=\cos(\theta-\beta),
\end{gather*}
由于两直角三角形是随便画的,上式两边的括号内一般不相等,那应该是相反(此处欠缺严谨),即
\[(\gamma+\theta-\alpha)+(\theta-\beta)=0\riff2\theta=\alpha+\beta-\gamma,\]
命题 1 得证。
(或许会有更简洁的证法还能更严谨,再说吧……)
接下来,在上图的基础上,我们继续画:
以 `OA` 为对称轴将 `\Rtt OAC` 对称到 `\Rtt OAC'`;
以 `OB` 为对称轴将 `\Rtt OBD` 对称到 `\Rtt OBD'`。
`D'C'` 的延长线与 `AB` 的延长线交于 `Q`,如下图:
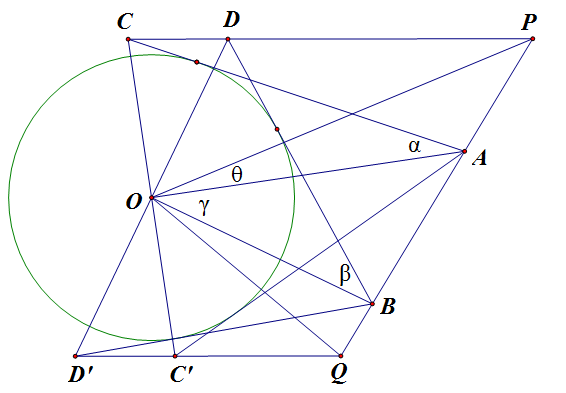
那么由上述命题,同样会得出 `2\angle BOQ=\alpha+\beta-\gamma`,于是得到:
推论 1:在上图中有:`\angle POA=\angle BOQ`。
要将上述结论运用到原题,还需要用到这帖:
forum.php?mod=redirect&goto=findpost& … =25195&ptid=2807
帖里的 6# 我证明了一个结论:
命题 2:设点 $A$ 在椭圆 $x^2/a^2+y^2/b^2=1$ 上,点 $B$ 在直线 $y=m$($m\ne0$)上,且 $OA\perp OB$,则:当 $1/a^2-1/b^2+1/m^2=0$ 时,直线 $AB$ 恒与 $x^2+y^2=b^2$ 相切。
这里 $1/a^2-1/b^2+1/m^2=0$ 化简下就是 `m=\pm ab/c`,正是 1# 原题的两条直线。
于是回到原题,过 `O` 作 `OA` 的垂线交那两直线于 `C`, `C'`,过 `O` 作 `OB` 的垂线交那两直线于 `D`, `D'`,如下图:
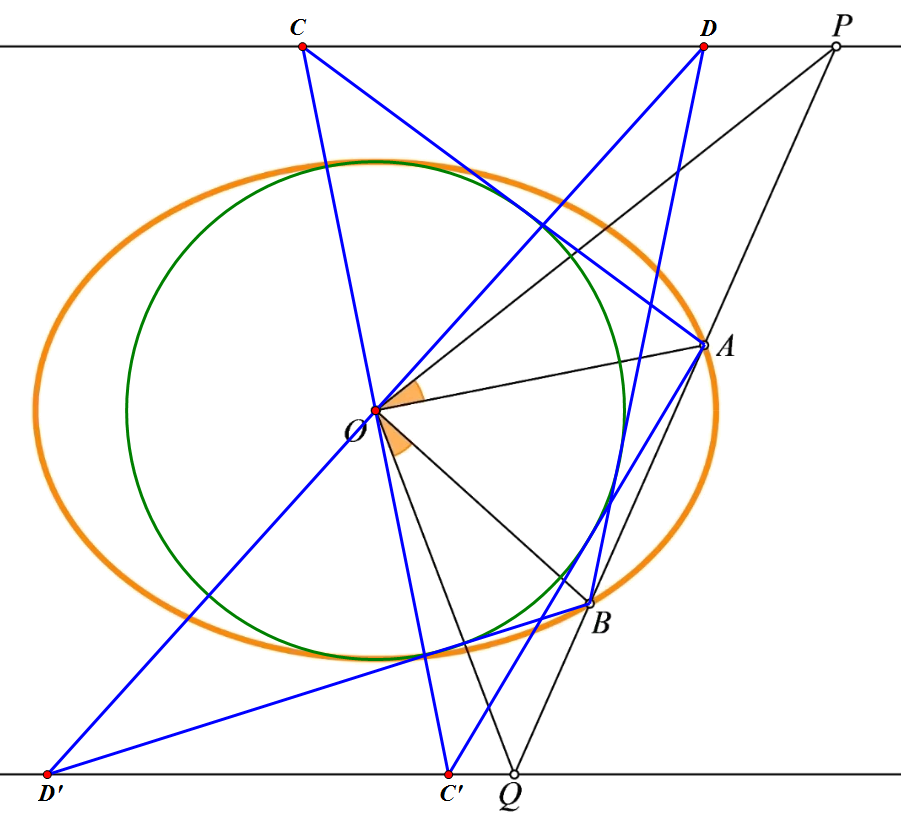
根据命题 2,`AC`, `AC'`, `BD`, `BD'` 均与圆 `x^2+y^2=b^2` 相切,于是由推论 1 即得 `\angle POA=\angle BOQ`。 |
Rate
-
View Rating Log
|