双曲线渐近线五点共圆

1+1=？

知乎一道五点共圆
题目：从双曲线上一点$P$作切线交双曲线的渐近线于$A,B$二点，再过点$P$作垂直$AB$的直线交双曲线对称轴于$C,D$二点，$O$为双曲线中心，证明$O,A,B,C,D$五点共圆.

1+1=？

证明如下：
先给出引理：凸四边形$OAFB$中，若$\angle F=\pi-\frac{1}{2}\angle O$且$\angle F和\angle O$是对角，则$\triangle AFB$的外心在$\triangle AOB$的外接圆上.
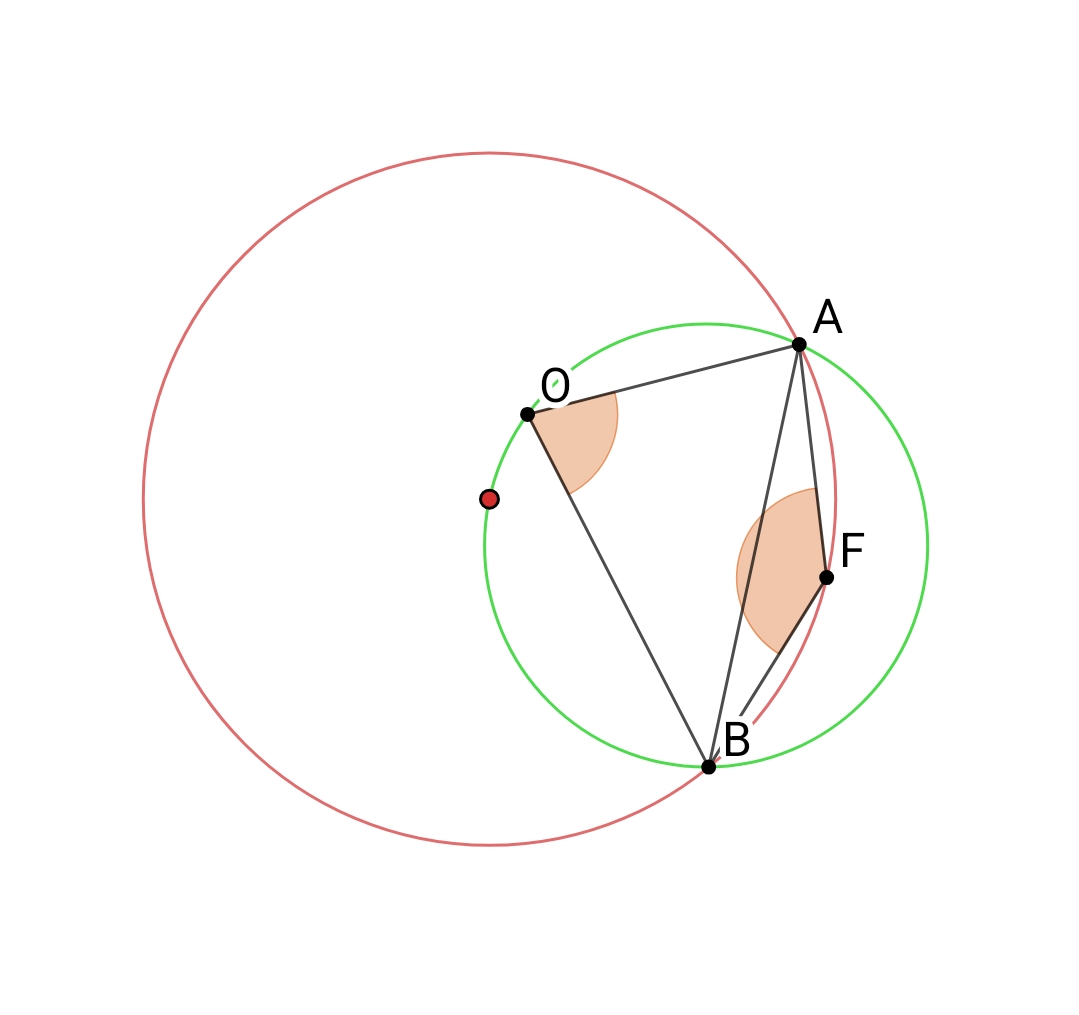
引理是易证的.
$(1)$证明：$\angle AFB=\pi-\frac{1}{2}\angle AOB$：
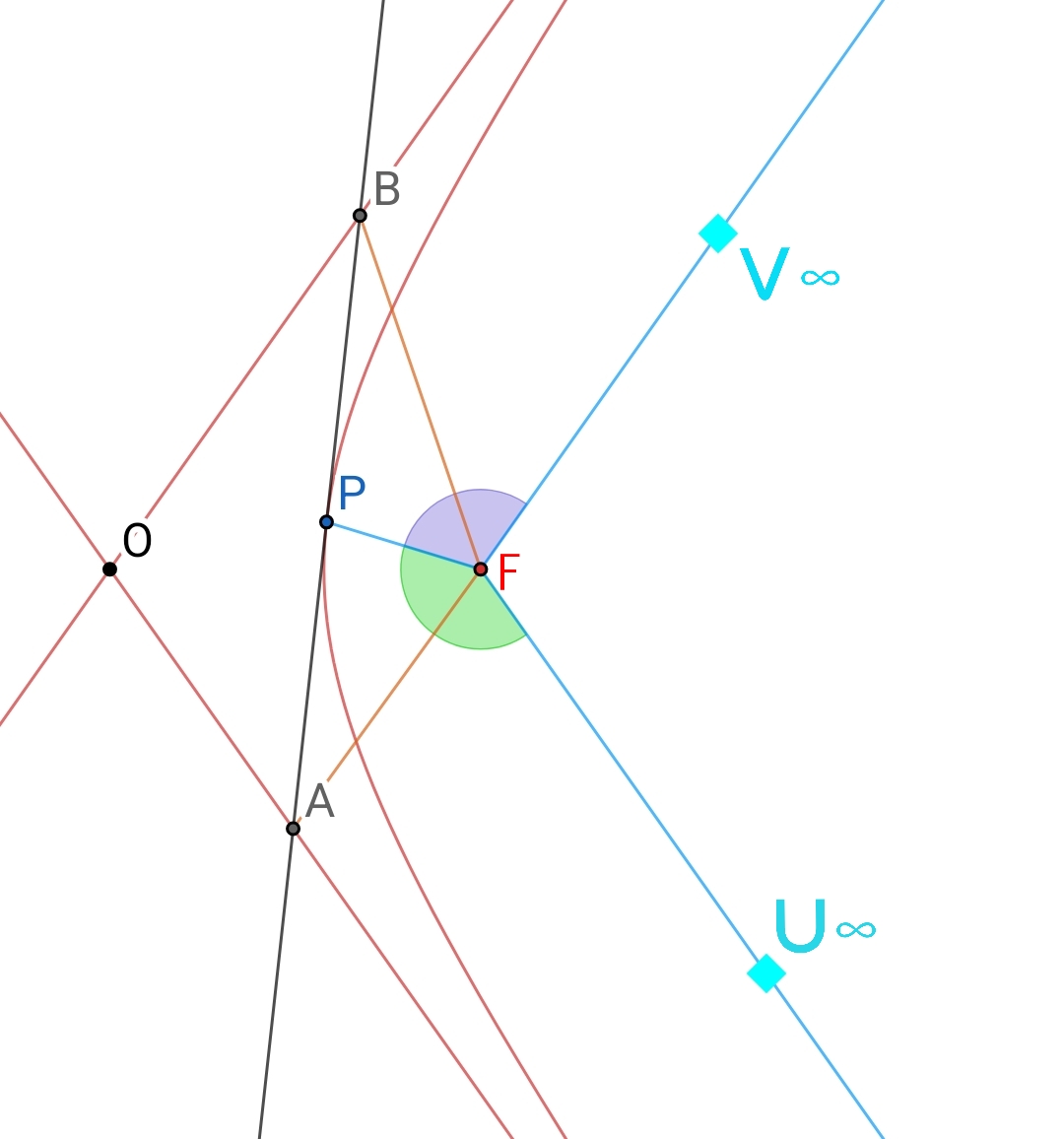
设渐近线$OA,OB$分别与双曲线相切于无穷远点$U,V$，可知$FU\px OA$，$FV\px OB$，由锥线的等角定理可知$FA$平分$\angle PFU$，$FB$平分$\angle PFV$.所以$\angle AFB=\frac{1}{2}(\angle PFU+\angle PFV)=\frac{1}{2}(2\pi-\angle UFV)=\pi-\frac{1}{2}\angle AOB$;
$(2)$证明$PC$是$AB$的中垂线：
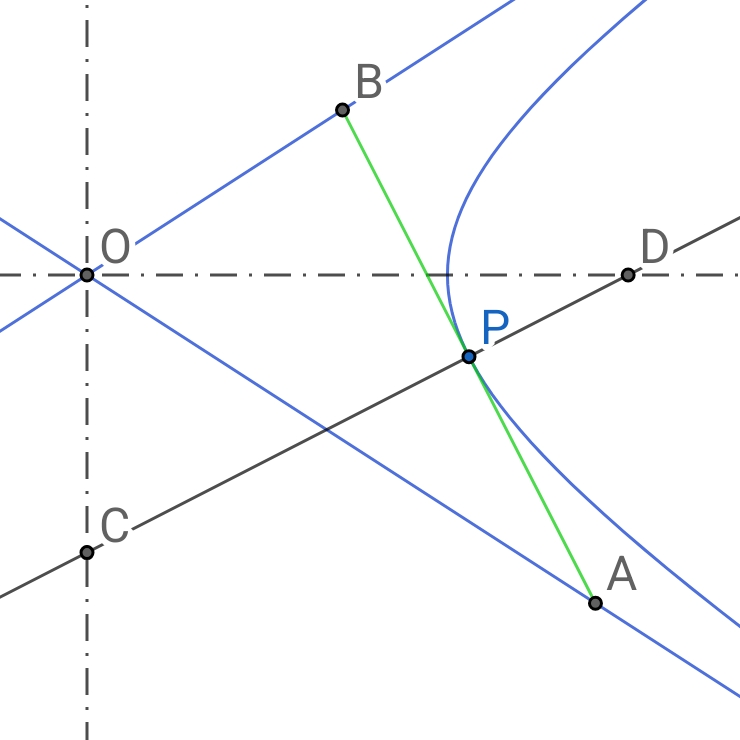
熟知双曲线上$P$点的切线交渐近线于$A,B$二点，则$P$是$AB$中点，且$PC$垂直$AB$，故$PC$是$AB$的中垂线；

$(3)$由引理知$\odot AFB$的圆心在$\odot AOB$上，由$PC$是$AB$的中垂线知$\odot AFB$的圆心在$PC$上，故$\odot AFB$的圆心在$PC$和$\odot AOB$的交点上，即$\odot AFB$的圆心是点$C$或点$D$，又$\angle AFB=\pi-\frac{1}{2}\angle AOB>\frac{\pi}{2}$，由钝角三角形的外心在钝角内部知点$C$是$\odot AFB$的圆心，故点$C$在$\odot AOB$上，同时有$\angle ACB=\angle AOB$；

$(4)$由$PC$平分$\angle ACB$，$OD$平分$\angle AOB$知$\angle AOD=\angle ACD$，故$A,O,C,D$四点共圆，又$A,O,B,C$四点共圆，故$A,O,B,C,D$五点共圆.

1+1=？

从证明中可知
从双曲线上一点$P$作切线和法线，切线交渐近线于$A,B$二点，法线交虚轴于$C$点，则$△ABC$是以$\angle C$为顶角且大小恒定的等腰三角形。当双曲线渐近线夹角为$60⁰$时，$△ABC$是正三角形。