|
|
 kuing
kuing
posted 2025-6-21 22:40
Last edited by kuing 2025-6-21 23:12没那么简单。
就比如改成 `\abs{y-x}\leqslant3`,道路加宽后,5# 图中能到达 `(n+1,n)` 的就不止红绿那两条线,还可以是 `(n+1,n-2)\to(n+1,n-1)\to(n+1,n)`,而 `(n+1,n-2)` 是多少还不知道,情况就不一样了。
我想了一下,对于 `\abs{y-x}\leqslant3`,如图:
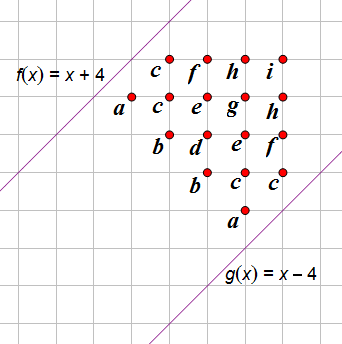
图中的字母表示原点到该点的路径数,这些数的关系就类似于杨辉三角那样,所以有
\begin{align*}
d&=b+b=2b,\\
g&=e+e=c+2d+c=a+3b+3b+a=2a+6b,\\
i&=c+3e+3e+c=4c+6d+4c=4a+10b+10b+4a=8a+20b,
\end{align*}
由此可得
\[i=4g-2d,\]
因此递推关系是
\[S_{n+2}=4S_{n+1}-2S_n,\]
然后由 `S_1=2`, `S_2=6`,求得
\[S_n=\frac{\bigl(2+\sqrt2\bigr)^n+\bigl(2-\sqrt2\bigr)^n}2,\]
它的前十项为 2, 6, 20, 68, 232, 792, 2704, 9232, 31520, 107616,哪位编程大佬写个程序验证一下……
另外我猜想 `\abs{y-x}\leqslant k` 的递推应该会是 `k-1` 阶线性递推,但像上面这样一步步推似乎有点笨,估计还会有更简洁的方法…… |
|