知乎一双曲线简单性质伪装题

1+1=？

来自知乎知乎提问
如图，一条与双曲线交于$A,B$二点的定斜率直线上有一点$P$，过$P$点作一条与渐近线平行的直线交另一条渐近线于$C$点，交双曲线于$D$点，则有$$\frac{PA \cdot PB}{OC \cdot PD}=\frac{(\sin \alpha)^2}{\sin \beta \cdot \sin \gamma}$$.

1+1=？

证明如下：(以下均用有向线段表示线段)
第一步先证明一个简单性质：一条定斜率直线与双曲线渐近线$\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=0$交于$F,G$二点，与双曲线$\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1$交于$A$点,则$AF \cdot AG$为定值。如图所示 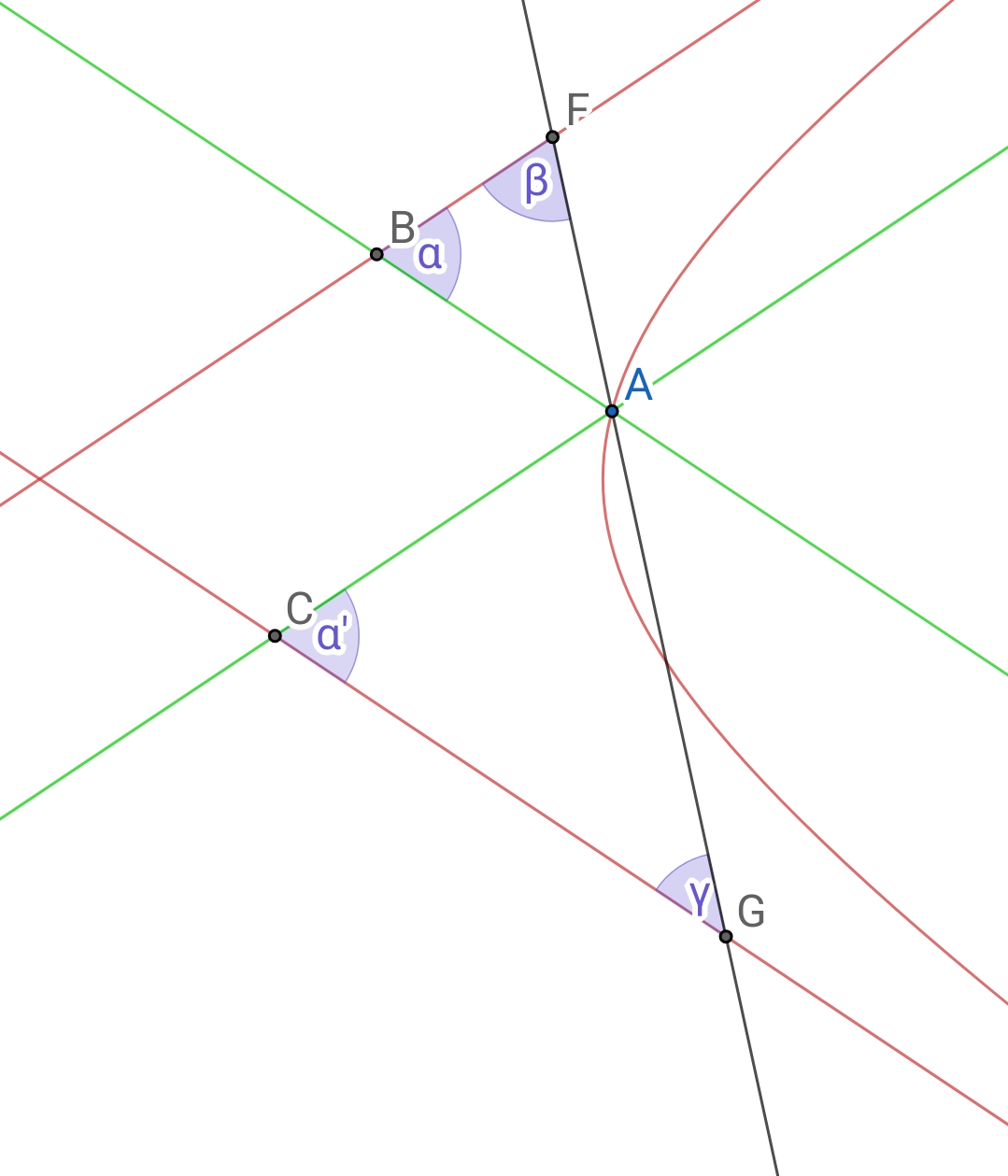以渐近线夹角为度规将点$A$分解到两条渐近线上即$B,C$二点，则$AF \cdot AG=\frac{AB sin\alpha}{sin\beta} \cdot \frac{ACsin\alpha}{sin\gamma}=\frac{(\sin \alpha)^2}{\sin \beta \cdot \sin \gamma} \cdot \frac{a^2+b^2}4$为定值。
第二步由直线AB交双曲线渐近线于$F,G$二点，易知$FA=BG$,即$PA \cdot PB=PF \cdot PG-AF \cdot AG$，如图所示
将点$P$分解到渐近线上得到$C,H$二点，设$PC$交双曲线于$D$点，过$D$作平行于$OF$的直线交$OH$于$K$点，则有$\frac{PF\cdot PG}{PC \cdot PH}=\frac{(\sin \alpha)^2}{\sin \beta \cdot \sin \gamma}=\frac{AF \cdot AG}{\frac{a^2+b^2}{4}}=\frac{PF \cdot PG-AF \cdot AG}{PC \cdot PH-CD \cdot PH}=\frac{PA \cdot PB}{PD \cdot PH}=\frac{PA \cdot PB}{PD \cdot OC}$,证毕！

1+1=？

此题还能再度伪装，如以下命题；
1.双曲线的定斜率弦$AB$(直线)上有一点$P$，过$P$作平行于双曲线渐近线的直线分别交双曲线及其渐近线于$D,C$二点，则$\frac{PA \cdot PB \cdot CD}{PD}$为定值。
2.双曲线的定斜率弦$AB$(直线)上有一点$P$，双曲线的中心为$O$点，直线$PO$与双曲线交于点$C$，则$\frac{PA \cdot PB}{|(\frac{PO}{OC})^2-1|}$为定值。
若直线$AB$与双曲线渐近线的夹角分别是$\gamma$,$\beta$，双曲线渐近线的夹角为$\alpha$，则该定值为$\frac{(\sin \alpha)^2}{\sin \beta \cdot \sin \gamma}\frac{a^2+b^2}4$.

其妙

图画得这么大，电脑浏览器打开把屏幕都占完了还看不清楚整个图