椭圆及其倒焦线的定角结论

1+1=？

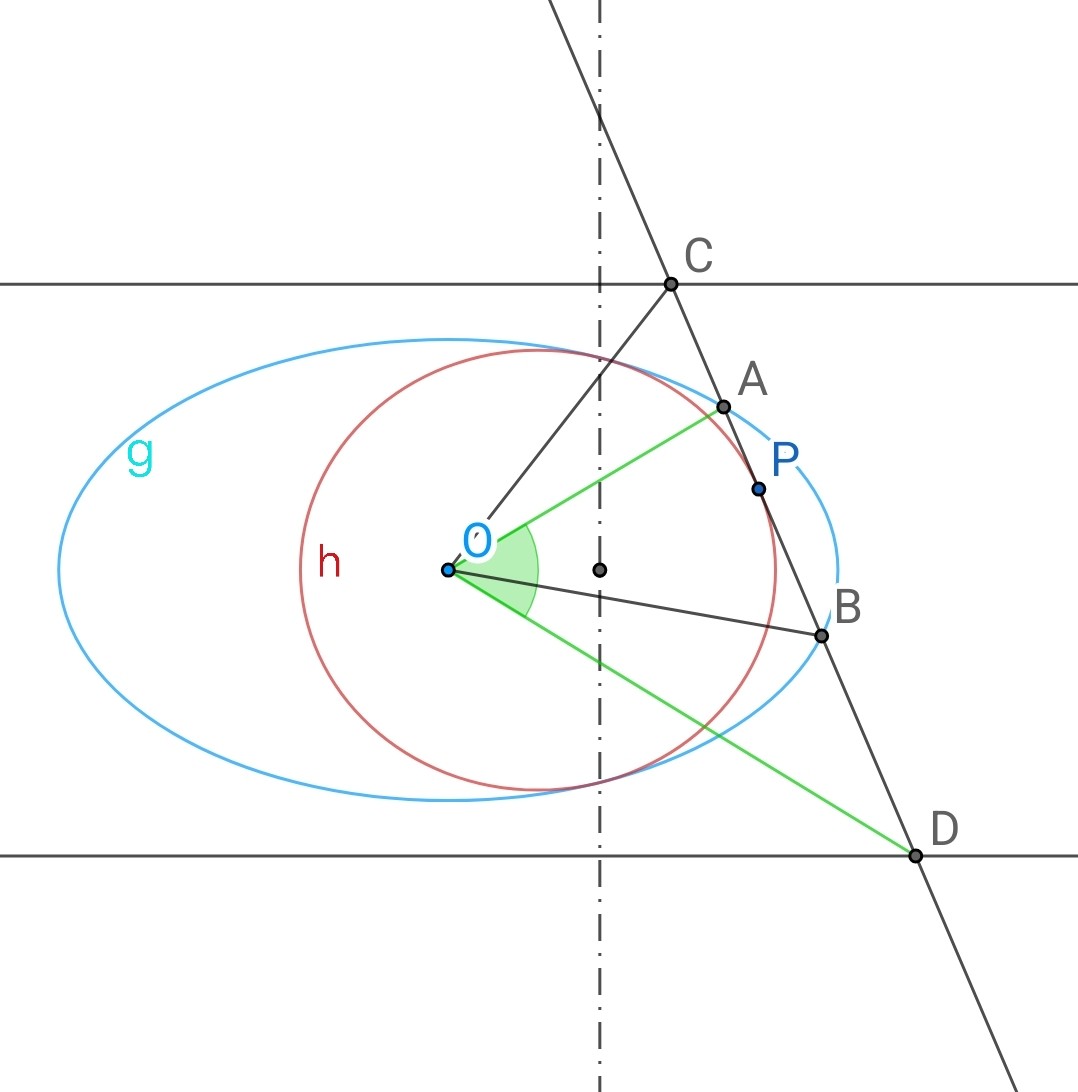
如图所示，已知椭圆$g$：$\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$，$O$为椭圆中心，直线$y=\dfrac{ab}{c},y=-\dfrac{ab}{c}$分别为该椭圆的倒焦线，则存在另一个与椭圆$g$有两个二重交点或一个三重交点的椭圆$h$，且$h$的一个焦点恰为$O$点，主轴平行于$g$。则作$h$上一点$P$的切线分别交椭圆$g$及其倒焦线于点$A,B；C,D$，($A,C$在$P$的一侧),则$\angle AOD=\angle BOC$且为定值。 $h$的方程为$a^{2} b^{2} m (2 b^{2} x+m (x^{2}-y^{2}))+a^{4} (-b^{4}+m^{2} y^{2}+b^{2} (-2 m x+x^{2}+y^{2}))=b^{4} m^{2} x^{2}$,其中$m$是二重交点的横坐标。
此结论是2014年北京卷理科第19题的推广。此结论应该还能再推广。