（z）正方体内放一个半球

realnumber

唐山 齐 11:41:33
在棱长为1的正方体内，放一个半球，其体积最大是多少？

乌贼

想当然，墙角处可以放任意大的球，只要保证正方体截面能包住球的大圆。

乌贼

回复 2# 乌贼
截面应垂直于$x+y+z=0$
是不是那个正六边形。还得大圆圆心到三墙面距离等于大圆半径。

realnumber

不是证明，半球的位置是猜测的：
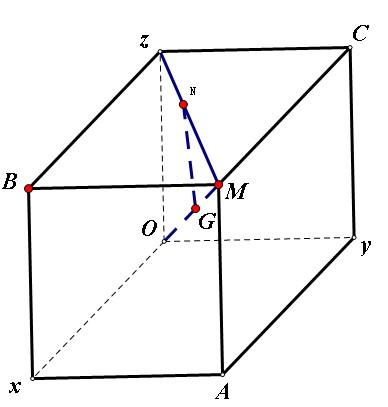
立方体表面与半球面上至少三个切点，且切点在两两相邻的三个面上.
如图，不妨设圆心为G，建坐标系后，坐标为(r,r,r),其中r为半径，
以下考虑半球与其它三个面的切点，过G且与OG垂直的一个平面是ABC,如此半球边沿与上底面BMC的切点N在面对角线上，NG⊥OG,NG=r,
如此在RtΔOMZ得$\frac{\sqrt{2}}{1}=\frac{\sqrt{3}-\sqrt{3}r}{r}$,解得$r=3-\sqrt{6}≈0.55051$

其妙

以前还有一个部分相似的题：
在长、宽均为1米、高为1分米的长方体空盒子内（不记厚度），装入直径为1分米的钢球，最多能装多少个？

realnumber

blog.sina.com.cn/s/blog_a329360c0101gieh.html

APPSYZY

先考虑一个简单的问题：有一个半径为$R$的半球和两个平行平面，平行平面和半球底面的夹角为定值$\theta$（相当于平行平面的法向量和半球底面法向量的夹角），若半球被夹在两个平面之间，不难证明两平面间距离的最小值为$R(1+\abs{\sin\theta})$.
回到楼主的问题，以正方体的一个顶点为原点，从这个顶点出发的三条棱为坐标轴建系，这三条坐标轴也就是正方体过这个顶点的三个面的法向量. 设半球底面的法向量与三条坐标轴的夹角分别为$\alpha,\beta,\gamma$，则由立体几何知识有
\[\sin^2\alpha+\sin^2\beta+\sin^2\gamma=2,\]
则
\[\max\{\abs{\sin\alpha},\abs{\sin\beta},\abs{\sin\gamma}\}\ge\sqrt{\frac23},\]
进而有正方体棱长
\[1\ge R\left(1+\sqrt{\frac23}\right),\]
得到最大半径$R_\max=3-\sqrt6$.

isee

回复 7# APPSYZY


厉害厉害，转载个图

realnumber

正方体AABCD-A’B‘C’D‘，半球O球心在体对角线AC'上，与以A为端点的三条面对角线相切(切点之一N)，与以C'为端点的三条面对角线相接(之一M)，
如图，截面AA’C‘C