旧论坛的一道未解决的积分题

kuing

原贴链接：kkkkuingggg.haotui.com/thread-967-1-1.html
原标题：证明积分不等式
原发贴人：reny

设 $f(x)$ 在 $[0,1]$ 上非负递增，求证：存在 $[0,1]$ 上的非负凸函数 $g(x)$ 满足 $g(x)\leqslant f(x)$ 且
\[
\int_0^1g(x)\rmd x\geqslant\frac12\int_0^1f(x)\rmd x.
\]

这里的凸是指下凸。

kuing

闲来无事翻旧帖……

1楼链接已失效，幸好当年存了档，现在把帖中我的想法截过来：

kuing

楼上最后这段，其实已经可以把 `g(x)` 具体写出来：

那直线系的包络可以看成当 `x` 取定而 `k` 变化时，使其值最大的点，也就是
\[g(x)=\max_{k\geqslant0}\bigl(kx+b(k)\bigr),\]而 `b(k)` 就是 `f(x)-kx` 的最小值，所以
\[g(x)=\max_{k\geqslant0}\Bigl( kx+\min_{t\in[0,1]}\bigl(f(t)-kt\bigr) \Bigr),\quad x\in[0,1],\]这就是 `g(x)` 的一种表达式，不过依然不知怎样证明原题。

当然，或许会有更好的表达式，又或者有更直接的证明原题的方法，继续顶。

kuing

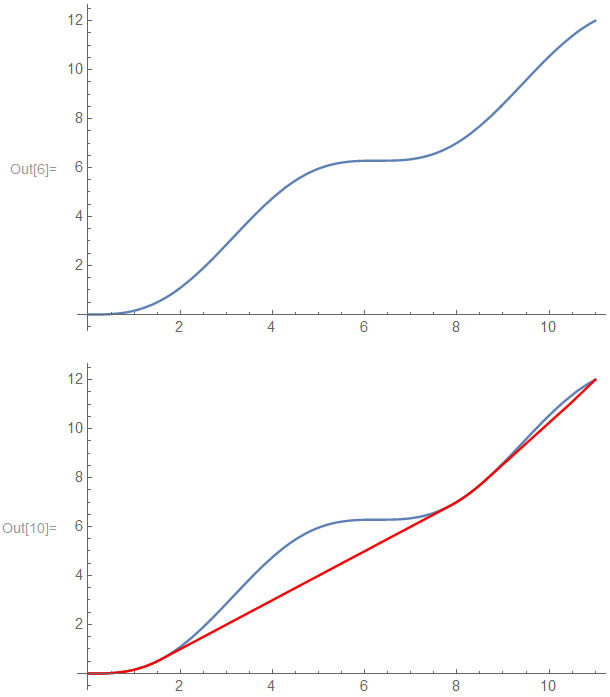
当年的图是用几何画板画的，画法已经忘记，刚才想用 Mathematica 按楼上的表达式来画一下，结果不太顺利，事关一般的函数求最小值并不简单，即使用 NMinValue 也不行，会弹出些不知啥提示然后卡死，结果还是自己想了个土办法，用 Min[Table[N[...],...]] 的方式取代 NMinValue，也就是等距取一堆点找最小。
下面以 `f(x)=x-\sin x`, `x\in[0,11]` 为示例如下：

1. f[x_] = x - Sin[x];
2. {xmin, xmax, nx} = {0, 11, 100};
3. {kmin, kmax, nk} = {0, 2, 20};
4. dx = (xmax - xmin)/nx;
5. dk = (kmax - kmin)/nk;
6. fx = Plot[f[x], {x, xmin, xmax}]
7. g[x_] := Max[Table[k x + Min[Table[N[f[t] - k t], {t, xmin, xmax, dx}]], {k, kmin, kmax, dk}]]
8. xgx = Table[{x, g[x]}, {x, xmin, xmax, dx}];
9. gx = ListLinePlot[xgx, PlotStyle -> Red];
10. Show[fx, gx]

复制代码

运行几秒后得：

另外，在软件中右键图片可以另存为 PDF，那是矢量图，可以放大看清楚。

orzweb111

This is an interesting property of convexity.  Intuitively, you got the clue of proving it. One could take $g(x)$ to be the lower part of the boundary curve of the convex hull of the curve $f(x)$.

orzweb111

There you go...