|
|
第一问略，只玩第二问。
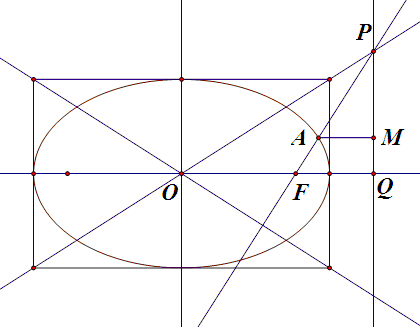
作 $PQ\perp x$ 轴于 $Q$，作 $AM\perp PQ$ 于 $M$。
由条件易知 $\angle FPQ=\angle POQ$，于是 $\triangle FPQ\sim\triangle POQ$，因此有
\[OQ\cdot FQ=PQ^2,\]
即
\[OQ\cdot (OQ-c)=\left( \frac ba\cdot OQ \right)^2,\]
解得
\[OQ=\frac c{1-\frac{b^2}{a^2}}=\frac{a^2}c,\]
可见直线 $PQ$ 就是椭圆的右准线，于是由第二定义及均值得
\begin{align*}
\frac{FA}{AP}&=\frac{e\cdot AM}{AP} \\
& =\frac{e\cdot PQ}{OP} \\
& =\frac{eb}{\sqrt{a^2+b^2}} \\
& =\frac{e\sqrt{a^2-c^2}}{\sqrt{2a^2-c^2}} \\
& =\sqrt{\frac{e^2(1-e^2)}{2-e^2}} \\
& =\sqrt{3-\left( 2-e^2+\frac2{2-e^2} \right)} \\
& \leqslant \sqrt{3-2\sqrt2} \\
& =\sqrt2-1,
\end{align*}
等号成立当且仅当 $(2-e^2)^2=2$，即 $e=\sqrt{2-\sqrt2}$。 |
|
isee
发表于 2014-1-6 21:23
