来自人教群的简单n元不等式

kuing

学生-caijinzhi(1349******) 12:14:38
大家好 我想问道题
已知Σxi=1,xi>0
求证

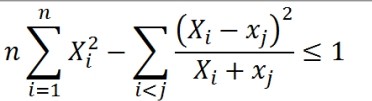
（X x不分大小写）
各位老师同学 爱好者 拜托了！
我的思路：在加一个(i<j)Σxixj把最左边凑成完全平方

\begin{align*}
n\sum_{i=1}^nx_i^2-\sum_{i<j}\frac{(x_i-x_j)^2}{x_i+x_j}\leqslant1&\iff n\sum_{i=1}^nx_i^2-\left( \sum_{i=1}^nx_i \right)^2\leqslant \sum_{i<j}\frac{(x_i-x_j)^2}{x_i+x_j} \\
&\iff\sum_{i<j}(x_i-x_j)^2\leqslant\sum_{i<j}\frac{(x_i-x_j)^2}{x_i+x_j},
\end{align*}
因为 $x_i+x_j<1$，故显然成立。

caijinzhi

Kuing大哥就是厉害！

Tesla35

Kuing大哥就是厉害！

其妙

Kuing小弟就是厉害！

kuing

你们两个水货……

其妙

回复 5# kuing
，的确那个恒等变形用的好啊！